
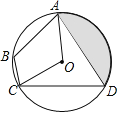
【题目】如图,已知⊙O的半径为2,四边形ABCD是⊙O的内接四边形,∠ABC=∠AOC,且AD=CD,则图中阴影部分的面积等于______.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
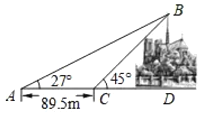
【题目】当地时间2019年4月15日下午,法国巴黎圣母院发生火灾,大火烧毁了巴黎圣母院后塔的塔顶.烧毁前,为测量此塔顶![]() 的高度,在地面选取了与塔底
的高度,在地面选取了与塔底![]() 共线的两点
共线的两点![]() 、
、![]() ,
,![]() 、
、![]() 在
在![]() 的同侧,在
的同侧,在![]() 处测量塔顶
处测量塔顶![]() 的仰角为27°,在
的仰角为27°,在![]() 处测量塔顶
处测量塔顶![]() 的仰角为45°,
的仰角为45°,![]() 到
到![]() 的距离是89.5米.设
的距离是89.5米.设![]() 的长为
的长为![]() 米,则下列关系式正确的是( )
米,则下列关系式正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
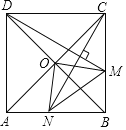
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个箱子内有![]() 颗相同的球,将
颗相同的球,将![]() 颗球分别标示号码
颗球分别标示号码![]() ,
,![]() ,
,![]() ,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球
,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球![]() 次,现已取了
次,现已取了![]() 次,取出的号码依次为
次,取出的号码依次为![]() ,
,![]() ,
,![]() ,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球
,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球![]() 次,则发生“这
次,则发生“这![]() 次得分的平均数在
次得分的平均数在![]() 之间(含
之间(含![]() ,
,![]() )”的情形的概率为________.
)”的情形的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上运动(不运动至两端点),射线
上运动(不运动至两端点),射线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的外接圆,连结
的外接圆,连结![]() ,
,![]() ,
,![]() .
.
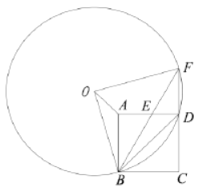
(1)求![]() 的度数.
的度数.
(2)求证:![]() .
.
(3)若正方形![]() 的边长为
的边长为![]() .
.
①当![]() 为
为![]() 中点时,求四边形
中点时,求四边形![]() 的面积.
的面积.
②设![]() ,
,![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 平分
平分![]() 时,
时,![]() _________(直接写出答案).
_________(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
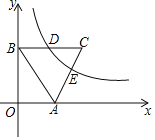
【题目】如图,在平面直角系中,点A在x轴正半轴上,点B在y轴正半轴上,∠ABO=30°,AB=2,以AB为边在第一象限内作等边△ABC,反比例函数的图象恰好经过边BC的中点D,边AC与反比例函数的图象交于点E.
(1)求反比例函数的解析式;
(2)求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
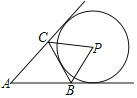
A.8B.10C.13D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
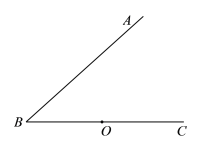
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com