
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
【答案】(1)MH=![]() ;(2)1个.
;(2)1个.
【解析】
(1)先根据题意补全图形,然后利用锐角三角函数求出圆的半径即OM的长度,再利用勾股定理求出BM的长度,最后利用![]() 可求出MH的长度.
可求出MH的长度.
(2)过点O作![]() ⊥
⊥![]() 于点
于点![]() ,通过等量代换可知∠
,通过等量代换可知∠![]() ∠
∠![]() ,从而利用角平分线的性质可知
,从而利用角平分线的性质可知![]() ,得出
,得出![]() 为⊙
为⊙![]() 的切线,从而可确定公共点的个数.
的切线,从而可确定公共点的个数.
解:(1)∵到点![]() 的距离等于线段
的距离等于线段![]() 的长的所有点组成图形
的长的所有点组成图形![]() ,
,
∴图形![]() 是以
是以![]() 为圆心,
为圆心,![]() 的长为半径的圆.
的长为半径的圆.
根据题意补全图形:
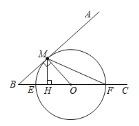
∵![]() 于点M,
于点M,
∴∠![]() .
.
在△![]() 中,
中,
![]() ,
,
∴![]() .
.
∵![]()
∴![]() ,
,
解得:![]() .
.
∴![]() .
.
在![]() △
△![]() 中,
中,
![]() ,
,
∴![]() .
.
∵![]()
∴![]()
∴![]() .
.
(2) 解: 1个.
证明:过点O作![]() ⊥
⊥![]() 于点
于点![]() ,
,
∵∠![]() ∠
∠![]()
![]() ,
,
且∠![]() ∠
∠![]()
![]() ,
,
∴ ∠![]() ∠
∠![]() .
.
∴![]() .
.
∴![]() 为⊙
为⊙![]() 的切线.
的切线.
∴射线![]() 与图形
与图形![]() 的公共点个数为1个.
的公共点个数为1个.



科目:初中数学 来源: 题型:
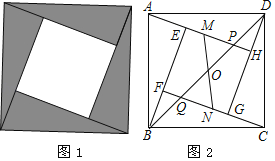
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作等边
的右侧作等边![]() .
.
(1)①如图1,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,则点
,则点![]() 到
到![]() 的距离是________;
的距离是________;
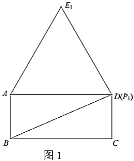
②如图2,当点![]() 运动到点
运动到点![]() 落在
落在![]() 上时,记等边
上时,记等边![]() 为等边
为等边![]() .则等边
.则等边![]() 的边长
的边长![]() 是________;
是________;
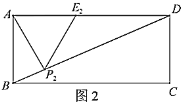
(2)如图3,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长;
的长;
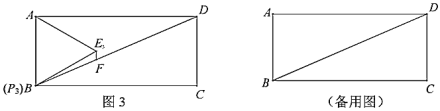
(3)①在上述变化过程中的点![]() ,
,![]() ,
,![]() 是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
②点![]() 的位置随着动点
的位置随着动点![]() 在线段
在线段![]() 上的位置变化而变化,猜想关于所有点
上的位置变化而变化,猜想关于所有点![]() 的位置的一个数学结论,试用一句话表述:______.
的位置的一个数学结论,试用一句话表述:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
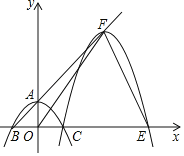
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .动点
.动点![]() 在
在![]() 上从点
上从点![]() 向终点
向终点![]() 匀速运动,同时,动点
匀速运动,同时,动点![]() 在射线
在射线![]() .上从点
.上从点![]() 沿
沿![]() 方向匀速运动,当点
方向匀速运动,当点![]() 运动到EF的中点时,点
运动到EF的中点时,点![]() 恰好与点
恰好与点![]() 重合,点
重合,点![]() 到达终点时,
到达终点时,![]() ,
, ![]() 同时停止运动.
同时停止运动.
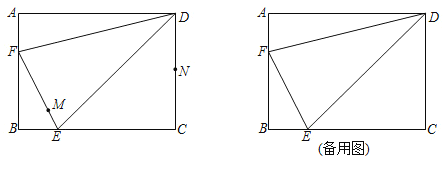
(1)求![]() 的长.
的长.
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变
的函数表达式,并写出自变![]() 的取值范围.
的取值范围.
(3)连接![]() ,当
,当![]() 与
与![]() 的一边平行时,求
的一边平行时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
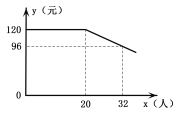
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com