
����Ŀ����֪������![]() �У�
��![]() ��
��![]() ����
����![]() �ǶԽ���
�ǶԽ���![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ����
����![]() ����
Ϊ����![]() ���Ҳ����ȱ�
���Ҳ����ȱ�![]() ��
��
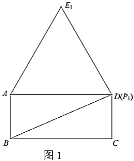
��1������ͼ1������![]() �˶������
�˶������![]() �غ�ʱ���ǵȱ�
�غ�ʱ���ǵȱ�![]() Ϊ�ȱ�
Ϊ�ȱ�![]() �����
�����![]() ��
��![]() �ľ�����________��
�ľ�����________��
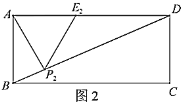
����ͼ2������![]() �˶�����
�˶�����![]() ����
����![]() ��ʱ���ǵȱ�
��ʱ���ǵȱ�![]() Ϊ�ȱ�
Ϊ�ȱ�![]() .��ȱ�
.��ȱ�![]() �ı߳�
�ı߳�![]() ��________��
��________��
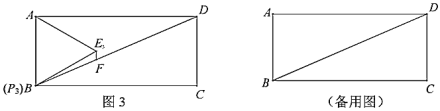
��2����ͼ3������![]() �˶������
�˶������![]() �غ�ʱ���ǵȱ�
�غ�ʱ���ǵȱ�![]() Ϊ�ȱ�
Ϊ�ȱ�![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ij���
�ij���
��3�����������仯�����еĵ�![]() ��
��![]() ��
��![]() �Ƿ���ͬһֱ���ϣ��뽨��ƽ��ֱ������ϵ�����жϣ���˵�����ɣ�
�Ƿ���ͬһֱ���ϣ��뽨��ƽ��ֱ������ϵ�����жϣ���˵�����ɣ�
�ڵ�![]() ��λ�����Ŷ���
��λ�����Ŷ���![]() ���߶�
���߶�![]() �ϵ�λ�ñ仯���仯������������е�
�ϵ�λ�ñ仯���仯������������е�![]() ��λ�õ�һ����ѧ���ۣ�����һ�仰������______��
��λ�õ�һ����ѧ���ۣ�����һ�仰������______��
���𰸡���1����![]() ����
����![]() ����2��
����2��![]() ����3���ٵ�
����3���ٵ�![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ����ɼ��������ڵ�
��ͬһ��ֱ���ϣ����ɼ��������ڵ�![]() ����ͬһ���߶Σ���ֱ�ߣ��ϣ�
����ͬһ���߶Σ���ֱ�ߣ��ϣ�
��������
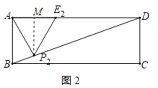
��1���ٹ���E1��E1N��BC��N����AD��M����MN��AB��![]() ���ɵȱ������ε����ʵó�AP1��AE1��AD��8��AM��4��E1M��
���ɵȱ������ε����ʵó�AP1��AE1��AD��8��AM��4��E1M��![]() �����ɵó��𰸣�
�����ɵó��𰸣�
����P2M��AD��M����P2M��AB����ȱ���AP2E2�ı߳�AE2Ϊ2x���ɵȱ������ε����ʵó�AP2��AE2��2x��AM��x��P2M��![]() ������P2MD�ס�BAD���ó�
������P2MD�ס�BAD���ó�![]() �������ó��𰸣�
�������ó��𰸣�
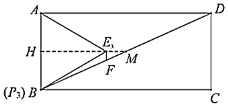
��2����![]() ��
��![]() �ڵ�
�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ���ɵȱ������ε����ʵó�
���ɵȱ������ε����ʵó�![]() ��
��![]() �����HM��
�����HM��![]() AD��4����ƽ���߷��߶γɱ����ó�
AD��4����ƽ���߷��߶γɱ����ó�![]() �����ɵó��𰸣�
�����ɵó��𰸣�
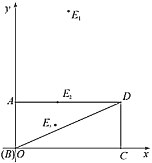
��3����BΪ����ԭ�㣬��BC����ֱ��Ϊx�ᣬAB����ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ���ɣ�1����2���ã�![]() ��
��![]() ��
��![]() ���ɴ���ϵ���������E1��E3��ֱ�߽���ʽ������E2������֤���ɵó����ۣ�
���ɴ���ϵ���������E1��E3��ֱ�߽���ʽ������E2������֤���ɵó����ۣ�
���ɢټ��ɵó����ۣ�
�⣺��1���١��ı���ABCD�Ǿ��Σ�
��BC��AD��8������E1��E1N��BC��N����AD��M����ͼ1��ʾ��
��MN��AB��![]() ��
��
���ı���ABCD�Ǿ��Σ�
��AD��BC��8��
�ߡ�AP1E1�ǵȱ������Σ�
��AP1��AE1��AD��8��AM��4��
��E1M��![]() ��
��
��E1N��![]() ������
������![]() ��
��![]() �ľ�����
�ľ�����![]() ��
��
����P2M��AD��M����ͼ2��ʾ����P2M��AB��
��ȱ���AP2E2�ı߳�AE2��2x��
��AP2��AE2��2x��AM��x��P2M��![]() ��
��
��P2M��AB��
���P2MD�ס�BAD��
��![]() ����
����![]() ��
��
��ã�x��![]() ��
��
��AE2��2x��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����![]() ��
��![]() �ڵ�
�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��3������![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ����ֱ��Ϊ
����ֱ��Ϊ![]() �ᣬ
�ᣬ![]() ����ֱ��Ϊ
����ֱ��Ϊ![]() �ᣬ����ƽ��ֱ������ϵ��
�ᣬ����ƽ��ֱ������ϵ��
�ɣ�1���٢ڣ�2������![]() ��
��![]() ��
��![]() ��
��
�辭��![]() ��
��![]() ��ֱ�߽���ʽΪ
��ֱ�߽���ʽΪ![]()
![]() ��
��
�����⣬�� �����
�����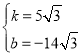 ��
��
��![]() ��
��
��![]() ����һ�κ�������ʽ����
����һ�κ�������ʽ����![]() ��
��
���![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�
����һ�仰��������![]() ����ͬһ���߶Σ���ֱ�ߣ��ϣ�
����ͬһ���߶Σ���ֱ�ߣ��ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������![]() ����ͬ����
����ͬ����![]() ����ֱ��ʾ����
����ֱ��ʾ����![]() ��
��![]() ��
��![]() ����ƺ���ÿ�δ�������ȡһ������ȡ��Żصķ�ʽ��ȡ����Ԥ��ȡ��
����ƺ���ÿ�δ�������ȡһ������ȡ��Żصķ�ʽ��ȡ����Ԥ��ȡ��![]() �Σ�����ȡ��
�Σ�����ȡ��![]() �Σ�ȡ���ĺ�������Ϊ
�Σ�ȡ���ĺ�������Ϊ![]() ��
��![]() ��
��![]() ����ÿ��ȡ��ʱ����һ����ȡ���Ļ������ȣ���ȡ���ĺ��뼴Ϊ�÷������ƺƴ������ƻ�����������ȡ��
����ÿ��ȡ��ʱ����һ����ȡ���Ļ������ȣ���ȡ���ĺ��뼴Ϊ�÷������ƺƴ������ƻ�����������ȡ��![]() �Σ���������
�Σ���������![]() �ε÷ֵ�ƽ������
�ε÷ֵ�ƽ������![]() ֮�䣨��
֮�䣨��![]() ��
��![]() ���������εĸ���Ϊ________��
���������εĸ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BC��4����P���ABC�ı�ߵ��ӳ������У�����P�뾶Ϊ2����ABC�����Ϊ5�����ABC���ܳ�Ϊ( )
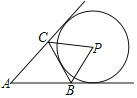
A.8B.10C.13D.14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
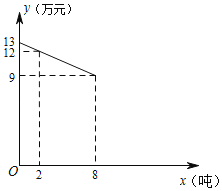
����Ŀ�����ݲ�ɽ��÷�����й���ij��˾��Ӫ��ɽ��÷ҵ����3��Ԫ/�ֵļ۸�������÷����װ��ֱ�����ۣ���װ�ɱ�Ϊ1��Ԫ/�֣�����ƽ�����ۼ۸�y����λ����Ԫ/�֣�����������x��2��x��10����λ���֣�֮��ĺ�����ϵ��ͼ��ʾ��
��1������÷��������Ϊ6��ʱ������ƽ�����ۼ۸���ÿ�ֶ�����Ԫ��
��2������������Ϊ����ʱ���þ�Ӫ������÷����õ�ë����w��������ë����Ϊ������Ԫ����ë�������������멁�����ܳɱ�����װ�ܷ��ã�
��3�������г����鷢�֣���÷��ӹ���װֱ�����ۣ�ƽ�����ۼ۸�Ϊ12��Ԫ/�֣���ӹ�����y����λ����Ԫ����ӹ�����x����λ���֣�֮��ĺ�����ϵ��y��![]() x+3��2��x��10����
x+3��2��x��10����
�����ù�˾������÷���ٶ�ʱ��������ӹ���ʽ��ֱ�Ӱ�װ���ۻ��ë����һ����
���ù�˾������÷�������� ����Χʱ��������ӹ���ʽ��ֱ�Ӱ�װ���ۻ��ë�����Щ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
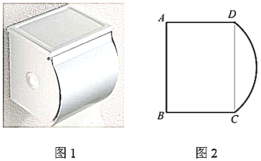
����Ŀ����ͼ1��һ��ֽ���У��ɺ�����Բ������ɣ�ͨ��Բ���ǵ���ת������ֽ���У���ͼ2��������ʾ��ͼ����֪����![]() �ij�
�ij�![]() ����
����![]() ��Բ���ǰ����
��Բ���ǰ����![]() ����Բ��Բ��
����Բ��Բ��![]() �Ǿ���
�Ǿ���![]() �����ģ��Ƶ�
�����ģ��Ƶ�![]() ��ת���أ����н������С�����һλ����
��ת���أ����н������С�����һλ����
 ������
������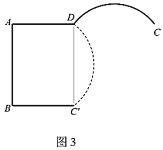
��1����![]() ����
����![]() �İ뾶����
�İ뾶����![]() ���Ե�Բ�ĽǶ�����
���Ե�Բ�ĽǶ�����
��2����ͼ3����Բ���ǰ����![]() ����ʼλ��
����ʼλ��![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() ʱ����
ʱ����![]() �������ת������ɨ���ĵ������
�������ת������ɨ���ĵ������
�ο����ݣ�![]() ��
��![]() ��
��![]() ȡ3.14��
ȡ3.14��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
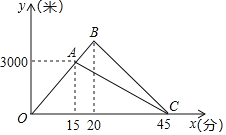
����Ŀ�������Ͱְֵ���������ַ���˶�������ͬʱ�Ӽҳ���������ͬ·��ǰ�У�;�аְ����·��أ���������ǰ��5���Ӻ�Ҳԭ·���أ�����ǡ��ͬʱ���������Ͱְ��������˶���������ҵ�·��y1���ף���y2���ף����˶�ʱ��x���֣�֮��ĺ�����ϵ��ͼ��ʾ
��1����ְַ���ʱ��ҵ�·��y2���ף����˶�ʱ��x���֣�֮��ĺ�����ϵʽ��
��2��������ʼ����ʱ��ְ��������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
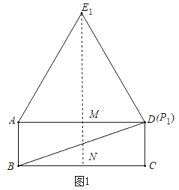
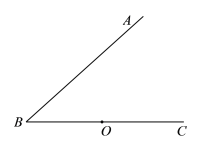
����Ŀ����ͼ����OΪ��ABC�ı�![]() �ϵ�һ�㣬����O��OM��AB�ڵ�
�ϵ�һ�㣬����O��OM��AB�ڵ�![]() ������
������![]() �ľ�������߶�OM�ij������е����ͼ��
�ľ�������߶�OM�ij������е����ͼ��![]() ��ͼ��W������
��ͼ��W������![]() ����E��F����(���ڵ�F�����).
����E��F����(���ڵ�F�����).
��1������![]() ��
��![]() �ڵ�
�ڵ�![]() �����BE=2��
�����BE=2��![]() ����MH�ij���
����MH�ij���
��2��������BC�Ƶ�B˳ʱ����ת�õ�����BD��ʹ�á�![]()
![]() ���ж�����BD��ͼ��
���ж�����BD��ͼ��![]() ������ĸ�������֤����
������ĸ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʯ���ڴ������Ҽ��������������У��̻����β���������ijУ�ƻ�����A��B������ľ��100�ý���У�̻����������г����飺����A����ľ2�ã�B����ľ5�ã�����600Ԫ������A����ľ3�ã�B����ľ1�ã�����380Ԫ��
��1����A�֣�B����ľÿ�ø�����Ԫ��
��2������Ҫ������A����ľ������������B����ľ������3����ѧУ���б깫˾ǩ���ĺ�ͬ�й涨�����г��۸������£��������������أ���ʵ�ʸ����ܽ��г��۾����Żݣ������һ�ֹ�����ľ�ķ�����ʹʵ������������ʡ���������ʡ�ķ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
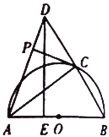
����Ŀ����ͼ����֪![]() ����
����![]() Ϊֱ������Բ
Ϊֱ������Բ![]() ���뾶
���뾶![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�õ�
˳ʱ����ת�õ�![]() ����
����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ������
������![]() ���
���![]() �غ�ʱֹͣ������
�غ�ʱֹͣ������![]() ���ӳ�����
���ӳ�����![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��
��1��![]() ______��
______��
��2����ͼ������![]() ���
���![]() �غ�ʱ���ж�
�غ�ʱ���ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�

��3����ͼ����![]() ʱ����
ʱ����![]() �ij���
�ij���

��4����ͼ������![]() ���߶�
���߶�![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() ���Բ
���Բ![]() ����ʱ��ֱ��д��ֱ��
����ʱ��ֱ��д��ֱ��![]() ��
��![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com