
【题目】如图,已知![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,半径
,半径![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当点
,当点![]() 与点
与点![]() 重合时停止.连接
重合时停止.连接![]() 并延长到点
并延长到点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() ______;
______;
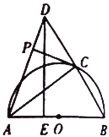
(2)如图,当点![]() 与点
与点![]() 重合时,判断
重合时,判断![]() 的形状,并说明理由;
的形状,并说明理由;

(3)如图,当![]() 时,求
时,求![]() 的长;
的长;

(4)如图,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 与半圆
与半圆![]() 相切时,直接写出直线
相切时,直接写出直线![]() 与
与![]() 的位置关系.
的位置关系.
【答案】(1)![]() ;(2)
;(2)![]() 是等边三角形,理由见解析;(3)
是等边三角形,理由见解析;(3)![]() 的长为
的长为![]() 或
或![]() ;(4)
;(4)![]()
【解析】
(1)先证AC垂直平分DB,即可证得AD=AB;
(2)先证AD=BD,又因为AD=AB,可得△ABD是等边三角形;
(3)分当点![]() 在
在![]() 上时和当点
上时和当点![]() 在
在![]() 上时,由勾股定理列方程求解即可;
上时,由勾股定理列方程求解即可;
(4)连结OC,证明OC∥AD, 由![]() 与半圆
与半圆![]() 相切,可得∠OCP=90°,即可得到
相切,可得∠OCP=90°,即可得到![]() 与
与![]() 的位置关系.
的位置关系.
解:(1)∵![]() 为直径,
为直径,
∴∠ACB=90°,
又∵![]()
∴AD=AB
∴![]() ,
,
故答案为10;
(2)![]() 是等边三角形,
是等边三角形,
理由如下:∵点![]() 与点
与点![]() 重合,∴
重合,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 是等边三角形;
是等边三角形;
(3)∵![]() ,∴
,∴![]() ,
,
当点![]() 在
在![]() 上时,
上时,
则![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中,
中,
由勾股定理得![]() ,即
,即![]() ,
,
解得![]() ,∴
,∴![]() ;
;
当点![]() 在
在![]() 上时,同理可得
上时,同理可得![]() ,
,
解得![]() ,∴
,∴![]() ,
,
综上所述,![]() 的长为
的长为![]() 或
或![]() ;
;
(4)![]() .
.
如图,连结OC,
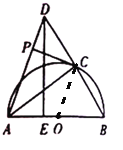
∵![]() 与半圆
与半圆![]() 相切,
相切,
∴OC⊥PC,
∵△ADB为等腰三角形,![]() ,
,
∴∠DAC=∠BAC,
∵AO=OC
∴∠CAO=∠ACO,
∴∠DAC=∠ACO,
∴OC∥AD,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作等边
的右侧作等边![]() .
.
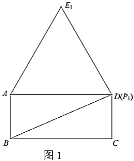
(1)①如图1,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,则点
,则点![]() 到
到![]() 的距离是________;
的距离是________;
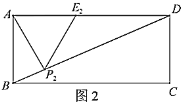
②如图2,当点![]() 运动到点
运动到点![]() 落在
落在![]() 上时,记等边
上时,记等边![]() 为等边
为等边![]() .则等边
.则等边![]() 的边长
的边长![]() 是________;
是________;
(2)如图3,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长;
的长;
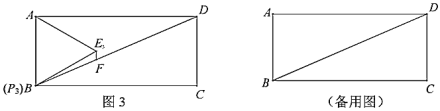
(3)①在上述变化过程中的点![]() ,
,![]() ,
,![]() 是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
②点![]() 的位置随着动点
的位置随着动点![]() 在线段
在线段![]() 上的位置变化而变化,猜想关于所有点
上的位置变化而变化,猜想关于所有点![]() 的位置的一个数学结论,试用一句话表述:______.
的位置的一个数学结论,试用一句话表述:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
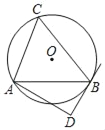
【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
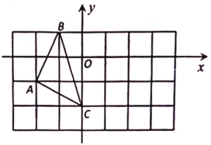
(1)点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标为______;
对称的点的坐标为______;
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;
;
(3)在(2)中,求边![]() 所扫过区域的面积是多少?(结果保留
所扫过区域的面积是多少?(结果保留![]() ).
).
(4)若![]() 、
、![]() 、
、![]() 三点的横坐标都加3,纵坐标不变,图形
三点的横坐标都加3,纵坐标不变,图形![]() 的位置发生怎样的变化?
的位置发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+3x+2与y轴交于点A,点B是抛物线的顶点,点C与点A是抛物线上关于对称轴对称的两个点,点D在x轴上运动,则四边形ABCD的两条对角线的长度之和的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
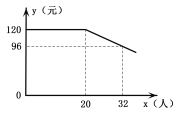
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一张斜边![]() 长为
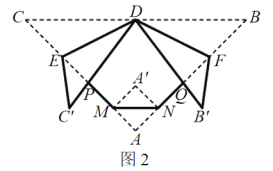
长为![]() 的等腰直角三角形纸片进行折“狗脸”活动(如图1所示) .第一步,如图2,沿
的等腰直角三角形纸片进行折“狗脸”活动(如图1所示) .第一步,如图2,沿![]() 向后折一个面积为1的等腰直角三角形
向后折一个面积为1的等腰直角三角形![]() ;第二步,在直角边
;第二步,在直角边![]() .上各取一点
.上各取一点![]() 为
为![]() 的中点,将
的中点,将![]() 分别沿
分别沿![]() 折叠,使得点
折叠,使得点![]() 对应点
对应点![]() 落在直线
落在直线![]() 上,
上,![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,则“狗脸”(图形
,则“狗脸”(图形![]() )的面积为__________.
)的面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com