
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,得出∠DGF=∠DFG.证出GD=DF.因此DG=GE=DF=EF,即可得出结论;
(2)连接DE,交AF于点O.由菱形的性质得出GF⊥DE,OG=OF=![]() GF.证明△DOF∽△ADF,得出
GF.证明△DOF∽△ADF,得出![]() ,即DF2=FOAF,即可得出结论;
,即DF2=FOAF,即可得出结论;
(3)作GH⊥CD于H,则CH=EG,由(1)得:AE=AD,在Rt△ABE中,由勾股定理得出BE=![]() =3,得出EC=2.设GF=x,菱形边长为y,则由(2)得:y2=
=3,得出EC=2.设GF=x,菱形边长为y,则由(2)得:y2=![]() x×AF①,在Rt△ADF中,AF2 =25+y2②,在Rt△ECF中,y2=4+(4y)2③,解得:y=
x×AF①,在Rt△ADF中,AF2 =25+y2②,在Rt△ECF中,y2=4+(4y)2③,解得:y=![]() ,代入②得:AF=
,代入②得:AF=![]() ,再代入①得:x=
,再代入①得:x=![]() 即可.
即可.
解:(1)∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF,
∴四边形EFDG为菱形.
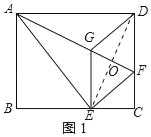
(2)如图1所示:连接DE,交AF于点O.
∵由(1)四边形EFDG为菱形.
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.
GFAF.
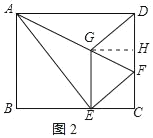
(3)作GH⊥CD于H,如图2所示:
则CH=EG,由(1)得:AE=AD,
在Rt△ABE中,AB=4,AE=AD=5,
∴BE=![]() =3,
=3,
∴EC=2.
设GF=x,菱形边长为y,则
由(2)得:y2=![]() x×AF①,
x×AF①,
在Rt△ADF中,AF2 =25+y2 ②
在Rt△ECF中,y2 =4+(4﹣y)2③
解得:y=![]() ,
,
代入②得:AF=![]() ,再代入①得:
,再代入①得:![]() .
.
即GF=![]() .
.


科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,半径
,半径![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当点
,当点![]() 与点
与点![]() 重合时停止.连接
重合时停止.连接![]() 并延长到点
并延长到点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() ______;
______;
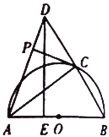
(2)如图,当点![]() 与点
与点![]() 重合时,判断
重合时,判断![]() 的形状,并说明理由;
的形状,并说明理由;

(3)如图,当![]() 时,求
时,求![]() 的长;
的长;

(4)如图,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 与半圆
与半圆![]() 相切时,直接写出直线
相切时,直接写出直线![]() 与
与![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
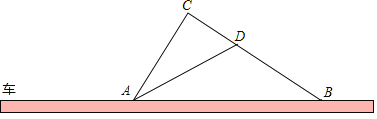
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现 对于2,4,6三个连续的偶数来说,可以得到![]() ;即前两个偶数的和等于第三个偶数;对于8,10,12,14,16五个连续的偶数来说,可以得到
;即前两个偶数的和等于第三个偶数;对于8,10,12,14,16五个连续的偶数来说,可以得到![]() ,即前三个偶数的和等于后两个偶数的和.…
,即前三个偶数的和等于后两个偶数的和.…
验证 对于九个连续偶数来说,若前五个偶数的和等于后四个偶数的和,则中间的偶数是_______;
延伸 是否存在连续的五个奇数,使得前三个奇数的和等于后两个奇数的和.若有,写出这五个奇数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
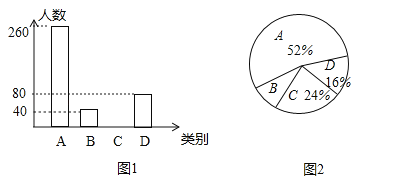
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 相交于
相交于![]() ,在直线
,在直线![]() 上分别取点
上分别取点![]() ,使
,使![]() ,分别过点A,B作直线
,分别过点A,B作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,设
,设![]() .
.
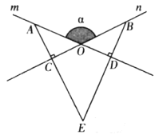
(1)求证:![]() ;
;
(2)小明说,不论![]() 是锐角还是钝角,点
是锐角还是钝角,点![]() 都在
都在![]() 的平分线上,你认为他说的有道理吗?并说明理由.
的平分线上,你认为他说的有道理吗?并说明理由.
(3)连接![]() ,当
,当![]() 与三角板的形状相同时,直接写出
与三角板的形状相同时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于直角坐标系 xOy 中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是___;
②点T在直线y=![]() x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线 y=﹣2x+2与x轴、y 轴分别交于点M、N,若线段MN上的所有点都是⊙C 的依附点,请求出圆心C的横坐标n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com