【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+2与y轴交于点A，点B是抛物线的顶点，点C与点A是抛物线上关于对称轴对称的两个点，点D在x轴上运动，则四边形ABCD的两条对角线的长度之和的最小值为_____．
科目：初中数学 来源： 题型：
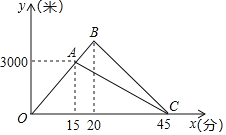
【题目】张琪和爸爸到曲江池遗址公园运动，两人同时从家出发，沿相同路线前行，途中爸爸有事返回，张琪继续前行5分钟后也原路返回，两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1（米），y2（米）与运动时间x（分）之间的函数关系如图所示
（1）求爸爸返问时离家的路程y2（米）与运动时间x（分）之间的函数关系式；
（2）张琪开始返回时与爸爸相距多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】焦作市教育局为调查全市教师的运动情况，结合现今流行的“微信运动”，随机调查了本市
名老师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表：
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
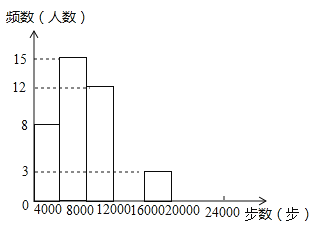
请根据以上信息，解答下列问题：
（1）写出
的值，并补全频数分布直方图；
（2）本市约有
名教师，结合调查的数据估计日行走步数超过
步（包含步）的教师有多少名？
（3）若在被调查的教师中，选取日行走步数超过
步（包含步）的两名教师与大家分享心得，求被选取的两名教师恰好都在
步（包含步）以上的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作
，交射线OB于点D，连接CD；
（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；
（3）连接OM，MN．
根据以上作图过程及所作图形，下列结论中错误的是（ ）
A. ∠COM=∠CODB. 若OM=MN，则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目：初中数学 来源： 题型：
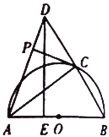
【题目】如图，已知
，以
为直径作半圆
，半径
绕点顺时针旋转得到
，点
的对应点为
，当点与点
重合时停止．连接
并延长到点
，使得
，过点作
于点
，连接
，
．
（1）
______；
（2）如图，当点与点重合时，判断
的形状，并说明理由；
（3）如图，当
时，求的长；
（4）如图，若点
是线段上一点，连接
，当与半圆相切时，直接写出直线与的位置关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知边长为4的正方形钢板有一个角锈蚀，其中AF＝2，BF＝1，为了合理利用这块钢板．将在五边形EABCD内截取一个矩形块MDNP，使点P在AB上，且要求面积最大，求钢板的最大利用率．
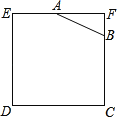
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】发现 对于2，4，6三个连续的偶数来说，可以得到
；即前两个偶数的和等于第三个偶数；对于8，10，12，14，16五个连续的偶数来说，可以得到
，即前三个偶数的和等于后两个偶数的和.…
验证 对于九个连续偶数来说，若前五个偶数的和等于后四个偶数的和，则中间的偶数是_______；
延伸 是否存在连续的五个奇数，使得前三个奇数的和等于后两个奇数的和.若有，写出这五个奇数；若没有，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图：
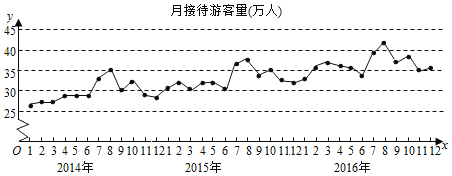
根据该折线图，下列结论错误的是（ ）
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7，8月份
D.各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
