练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

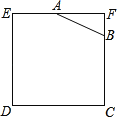
    【题目】如图所示，已知边长为4的正方形钢板有一个角锈蚀，其中AF＝2，BF＝1，为了合理利用这块钢板．将在五边形EABCD内截取一个矩形块MDNP，使点P在AB上，且要求面积最大，求钢板的最大利用率．

    【答案】80%

    【解析】

    根据题意画图分析．用含表示某一边的字母的代数式表示面积，关键是表示另一边的长．借助三角形相似建立关系．

    解：如图所示，为了表达矩形MDNP的面积，设DN＝x，PN＝y，

    则面积S＝xy①，

    ∵点P在AB上，由△APQ∽△ABF得，

    ，

    即x＝10﹣2y，

    ∴代入①，得S＝（10﹣2y）y＝﹣2y2+10y，

    即，

    因为3≤y≤4，而不在自变量的取值范围内，

    所以不是最值点，

    当y＝3时，S＝12；当y＝4时，S＝8，故面积的最大值是S＝12，此时，钢板的最大利用率是80%．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝40°，连接BD、CE．将△ADE绕点A旋转，BD、CE也随之运动．

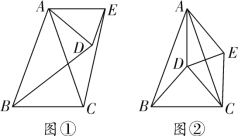
    （1）求证：BD＝CE；

    （2）在△ADE绕点A旋转过程中，当AE∥BC时，求∠DAC的度数；

    （3）如图②，当点D恰好是△ABC的外心时，连接DC，判断四边形ADCE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，抛物线y＝ax2+bx+c与x轴交于A、B两点，A（﹣5，0），与y轴交于C（0，﹣5），并且对称轴x＝﹣3．

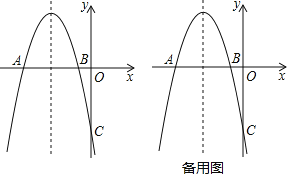
    （1）求抛物线的解析式；

    （2）P在x轴上方的抛物线上，过P的直线y＝x+m与直线AC交于点M，与y轴交于点N，求PM+MN的最大值；

    （3）点D为抛物线对称轴上一点，

    ①当△ACD是以AC为直角边的直角三角形时，求D点坐标；

    ②若△ACD是锐角三角形，求点D的纵坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图，图中为下水管道口直径，为可绕转轴自由转动的阀门，平时阀门被管道中排出的水冲开，可排出城市污水：当河水上涨时，阀门会因河水压迫而关闭，以防止河水倒灌入城中．若阀门的直径，为检修时阀门开启的位置，且．

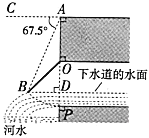
    （1）直接写出阀门被下水道的水冲开与被河水关闭过程中的取值范围；

    （2）为了观测水位，当下水道的水冲开阀门到达位置时，在点处测得俯角，若此时点恰好与下水道的水平面齐平，求此时下水道内水的深度．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+2与y轴交于点A，点B是抛物线的顶点，点C与点A是抛物线上关于对称轴对称的两个点，点D在x轴上运动，则四边形ABCD的两条对角线的长度之和的最小值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y1＝x+2与反比例函数y2＝的图象交于A，B两点，点A的坐标为（1，a）．

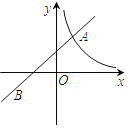
    （1）求出k的值及点B的坐标；

    （2）根据图象，写出y1＞y2时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在2019年植树节这一天，某校组织300名七年级学生，200名八年级学生，100名九年级学生参加义务植树活动.图甲是根据植树情况绘制成的条形统计图.

    请根据题中提供的信息解答下列问题.

    (1)参加植树的学生平均每人植树多少棵？

    (2)图2是小明同学尚未完成的各年级植树情况的扇形统计图，请你把它补充完整(要求标注圆心角度数)；

    (3)若该种树苗在正常情况下的成活率为85%，则今后还需补种多少棵树？(补种树苗的成活率也为85%)

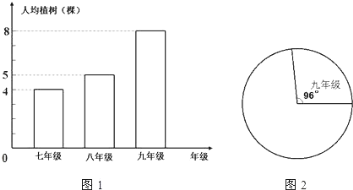
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程．

    已知：直线l及直线l上一点P．

    求作：直线PQ，使得PQ⊥l．

    作法：如图，

    ①在直线l上取一点A（不与点P重合），分别以点P，A为圆心，AP长为半径画弧，两弧在直线l的上方相交于点B；

    ②作射线AB，以点B为圆心，AP长为半径画弧，交AB的延长线于点Q；

    ③作直线PQ．

    所以直线PQ就是所求作的直线．

    根据小东设计的尺规作图过程，

    （1）使用直尺和圆规，补全图形；（保留作图痕迹）

    （2）完成下面的证明．

    证明：连接BP，

    ∵　 　＝　 　＝　 　＝AP，

    ∴点A，P，Q在以点B为圆心，AP长为半径的圆上．

    ∴∠APQ＝90°（　 　）．（填写推理的依据）

    即PQ⊥l．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，BC＝AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

    （1）求证：点D是AB的中点；

    （2）判断DE与⊙O的位置关系，并证明你的结论；

    （3）若⊙O的直径为10，tanB＝3，求DE的长．

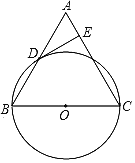
    查看答案和解析>>

    同步练习册答案