
ЁОЬтФПЁПЯТУцЪЧаЁЖЋЩшМЦЕФЁАЙ§жБЯпЩЯвЛЕузїетЬѕжБЯпЕФДЙЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
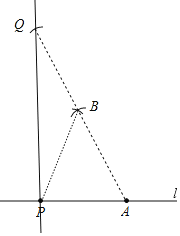
вбжЊЃКжБЯпlМАжБЯпlЩЯвЛЕуPЃЎ
![]()
ЧѓзїЃКжБЯпPQЃЌЪЙЕУPQЁЭlЃЎ
зїЗЈЃКШчЭМЃЌ
![]()
ЂйдкжБЯпlЩЯШЁвЛЕуAЃЈВЛгыЕуPжиКЯЃЉЃЌЗжБ№вдЕуPЃЌAЮЊдВаФЃЌAPГЄЮЊАыОЖЛЛЁЃЌСНЛЁдкжБЯпlЕФЩЯЗНЯрНЛгкЕуBЃЛ
ЂкзїЩфЯпABЃЌвдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЛЛЁЃЌНЛABЕФбгГЄЯпгкЕуQЃЛ
ЂлзїжБЯпPQЃЎ
ЫљвджБЯпPQОЭЪЧЫљЧѓзїЕФжБЯпЃЎ
ИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃЎ
жЄУїЃКСЌНгBPЃЌ
ЁпЁЁ ЁЁЃНЁЁ ЁЁЃНЁЁ ЁЁЃНAPЃЌ
ЁрЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯЃЎ
ЁрЁЯAPQЃН90ЁуЃЈЁЁ ЁЁЃЉЃЎЃЈЬюаДЭЦРэЕФвРОнЃЉ
МДPQЁЭlЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉBPЃЌBAЃЌBQЃЌжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌгУжБГпКЭдВЙцзїЭММДПЩЃЛ
ЃЈ2ЃЉжЄУїЫМТЗЮЊЃКгЩзїЭМЙ§ГЬПЩжЊ![]() ЃЌДгЖјПЩЕУЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯЃЌдйИљОндВжмНЧЖЈРэМДПЩжЄ.
ЃЌДгЖјПЩЕУЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯЃЌдйИљОндВжмНЧЖЈРэМДПЩжЄ.
ЃЈ1ЃЉИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌгУжБГпКЭдВЙцзїЭМНсЙћШчЯТЫљЪОЃК
ЃЈ2ЃЉжЄУїЃКСЌНгBP
![]()
ЁрЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯ
![]() ЃЈжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЉ
ЃЈжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЉ
МД![]()
ЙЪД№АИЮЊBPЃЌBAЃЌBQЃЛжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧ.


 ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+c(aЁй0)ЩЯВПЗжЕуЕФКсзјБъxгызнзјБъyЕФЖдгІжЕШчЯТБэЃК
x | Ё | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё |
| Љ4 |
| Љ4 |
| 0 |
| Ё |
(1)ЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
(2)вбжЊЕуE(4ЃЌ y)ЪЧИУХзЮяЯпЩЯЕФЕуЃЌЕуEЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЕФЕуЮЊЕуFЃЌЧѓЕуEКЭЕуFЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊБпГЄЮЊ4ЕФе§ЗНаЮИжАхгавЛИіНЧатЪДЃЌЦфжаAFЃН2ЃЌBFЃН1ЃЌЮЊСЫКЯРэРћгУетПщИжАхЃЎНЋдкЮхБпаЮEABCDФкНиШЁвЛИіОиаЮПщMDNPЃЌЪЙЕуPдкABЩЯЃЌЧввЊЧѓУцЛ§зюДѓЃЌЧѓИжАхЕФзюДѓРћгУТЪЃЎ
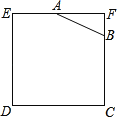
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
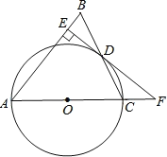
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌвдACБпЮЊжБОЖзї![]() OНЛBCБпгкЕуDЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЌEDЁЂACЕФбгГЄЯпНЛгкЕуF.
OНЛBCБпгкЕуDЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЌEDЁЂACЕФбгГЄЯпНЛгкЕуF.
(1)ЧѓжЄЃКEFЪЧ![]() OЕФЧаЯпЃЛ
OЕФЧаЯпЃЛ
(2)ШєEB=6ЃЌЧвsinЁЯCFD=![]() ЃЌЧѓ
ЃЌЧѓ![]() OЕФАыОЖ.
OЕФАыОЖ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗЂЯж Ждгк2ЃЌ4ЃЌ6Ш§ИіСЌајЕФХМЪ§РДЫЕЃЌПЩвдЕУЕН![]() ЃЛМДЧАСНИіХМЪ§ЕФКЭЕШгкЕкШ§ИіХМЪ§ЃЛЖдгк8ЃЌ10ЃЌ12ЃЌ14ЃЌ16ЮхИіСЌајЕФХМЪ§РДЫЕЃЌПЩвдЕУЕН
ЃЛМДЧАСНИіХМЪ§ЕФКЭЕШгкЕкШ§ИіХМЪ§ЃЛЖдгк8ЃЌ10ЃЌ12ЃЌ14ЃЌ16ЮхИіСЌајЕФХМЪ§РДЫЕЃЌПЩвдЕУЕН![]() ЃЌМДЧАШ§ИіХМЪ§ЕФКЭЕШгкКѓСНИіХМЪ§ЕФКЭ.Ё
ЃЌМДЧАШ§ИіХМЪ§ЕФКЭЕШгкКѓСНИіХМЪ§ЕФКЭ.Ё
бщжЄ ЖдгкОХИіСЌајХМЪ§РДЫЕЃЌШєЧАЮхИіХМЪ§ЕФКЭЕШгкКѓЫФИіХМЪ§ЕФКЭЃЌдђжаМфЕФХМЪ§ЪЧ_______ЃЛ
бгЩь ЪЧЗёДцдкСЌајЕФЮхИіЦцЪ§ЃЌЪЙЕУЧАШ§ИіЦцЪ§ЕФКЭЕШгкКѓСНИіЦцЪ§ЕФКЭ.ШєгаЃЌаДГіетЮхИіЦцЪ§ЃЛШєУЛгаЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпyЃНx+4гыХзЮяЯпyЃНЉ![]() x2+bx+cЃЈbЃЌcЪЧГЃЪ§ЃЉНЛгкAЁЂBСНЕуЃЌЕуAдкxжсЩЯЃЌЕуBдкyжсЩЯЃЎЩшХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊЕуCЃЎ
x2+bx+cЃЈbЃЌcЪЧГЃЪ§ЃЉНЛгкAЁЂBСНЕуЃЌЕуAдкxжсЩЯЃЌЕуBдкyжсЩЯЃЎЩшХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊЕуCЃЎ

ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгыЕуAЁЂBжиКЯЃЉЃЌ
ЂйШчЭМ2ЃЌШєЕуPдкжБЯпABЩЯЗНЃЌСЌНгOPНЛABгкЕуDЃЌЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЂкШчЭМ3ЃЌШєЕуPдкxжсЕФЩЯЗНЃЌСЌНгPCЃЌвдPCЮЊБпзїе§ЗНаЮCPEFЃЌЫцзХЕуPЕФдЫЖЏЃЌе§ЗНаЮЕФДѓаЁЁЂЮЛжУвВЫцжЎИФБфЃЎЕБЖЅЕуEЛђFЧЁКУТфдкyжсЩЯЃЌжБНгаДГіЖдгІЕФЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
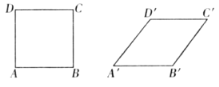
ЁОЬтФПЁПШчЭМЃЌжЛИФБфе§ЗНаЮ![]() ЕФаЮзДЃЌЕУЕНЫФБпаЮ
ЕФаЮзДЃЌЕУЕНЫФБпаЮ![]() ЃЌЧв
ЃЌЧв![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() гые§ЗНаЮ
гые§ЗНаЮ![]() ЕФУцЛ§ЕФБШЪЧЃЈ ЁЁЃЉ
ЕФУцЛ§ЕФБШЪЧЃЈ ЁЁЃЉ
A.1:1B.2:3C.![]() :2D.3:4
:2D.3:4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсНЛгкЕу
гыxжсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌгыyжсНЛгкЕуCЃЌЧвЙ§Еу
ЃЌгыyжсНЛгкЕуCЃЌЧвЙ§Еу![]() ЃЎЕуPЁЂQЪЧХзЮяЯп
ЃЎЕуPЁЂQЪЧХзЮяЯп![]() ЩЯЕФЖЏЕуЃЎ
ЩЯЕФЖЏЕуЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЕБЕуPдкжБЯпODЯТЗНЪБЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЃЎ
УцЛ§ЕФзюДѓжЕЃЎ
(3)жБЯпOQгыЯпЖЮBCЯрНЛгкЕуEЃЌЕБ![]() гы
гы![]() ЯрЫЦЪБЃЌЧѓЕуQЕФзјБъЃЎ
ЯрЫЦЪБЃЌЧѓЕуQЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЬНОПЃКШчЭМЃЌЖўДЮКЏЪ§![]() ОЙ§ЕуBЃЈ4ЃЌ0ЃЉКЭЕуEЃЈ-2ЃЌ-3ЃЉСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊAЃЎЕуDЪЧЯпЖЮBEЩЯЕФЖЏЕуЃЌЙ§ЕуDзїDFЁЭBEЃЌНЛyжсгкЕуFЃЌНЛХзЮяЯпгкЕуPЃЎ
ОЙ§ЕуBЃЈ4ЃЌ0ЃЉКЭЕуEЃЈ-2ЃЌ-3ЃЉСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊAЃЎЕуDЪЧЯпЖЮBEЩЯЕФЖЏЕуЃЌЙ§ЕуDзїDFЁЭBEЃЌНЛyжсгкЕуFЃЌНЛХзЮяЯпгкЕуPЃЎ
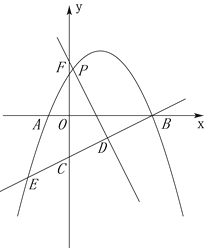
ЃЈ1ЃЉЧѓГіХзЮяЯпКЭжБЯпBEЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЁїDCFЁеЁїBOCЪБЃЌЧѓГіДЫЪБЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуPЕФКсзјБъЮЊmЃЎ
ЂйЧыаДГіЯпЖЮPDЕФГЄЖШЮЊЃЈгУКЌmЕФЪНзгБэЪОЃЉЃЛ
ЂкЕБmЮЊКЮжЕЪБЃЌЯпЖЮPDгазюДѓжЕЃЌВЂаДГіЦфзюДѓжЕЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com