
【题目】综合与探究:如图,二次函数![]() 经过点B(4,0)和点E(-2,-3)两点,与x轴的另一个交点为A.点D是线段BE上的动点,过点D作DF⊥BE,交y轴于点F,交抛物线于点P.
经过点B(4,0)和点E(-2,-3)两点,与x轴的另一个交点为A.点D是线段BE上的动点,过点D作DF⊥BE,交y轴于点F,交抛物线于点P.
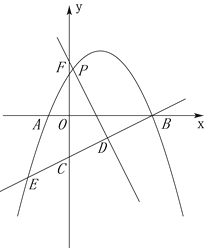
(1)求出抛物线和直线BE的解析式;
(2)当△DCF≌△BOC时,求出此时点D的坐标;
(3)设点P的横坐标为m.
①请写出线段PD的长度为(用含m的式子表示);
②当m为何值时,线段PD有最大值,并写出其最大值为多少?
【答案】(1)![]() ,y=
,y=![]() x-2;(2)点D的坐标为(
x-2;(2)点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)①
);(3)①![]() ;②当m=1时,PD有最大值为
;②当m=1时,PD有最大值为![]() .
.
【解析】
(1)设直线BE的解析式为y=kx+t,把B、E坐标分别代入![]() 和y=kx+t,求出b、c、k、t的值即可得答案;
和y=kx+t,求出b、c、k、t的值即可得答案;
(2)根据BE解析式可得C点坐标,利用勾股定理可求出BC的长,当点F在点C上方时,由全等三角形得性质可得OC=CD,过点D作DH⊥OB,垂足为H,可得DH//OC,根据平行线分线段成比例定理可得![]() ,可求出OH的长,代入BE解析式求出y值即可得点D坐标;同理可求出当点F在点C下方时点D的坐标;
,可求出OH的长,代入BE解析式求出y值即可得点D坐标;同理可求出当点F在点C下方时点D的坐标;
(3)①过点P作PQ//FC,交BE于Q,根据抛物线及BE解析式可用m表示出P、Q坐标,即可表示出PQ得长,根据平行线得性质可得∠OCB=∠PQD,可得∠PQD得正弦值,利用∠PQD的正弦即可表示出PD的长;
②根据二次函数得性质即可得答案.
(1)把B(4,0),E(-2,-3)代入抛物线的解析式得: ,
,
解得b=![]() ,c=2.
,c=2.
∴抛物线的解析式为![]() ,
,
设直线BE的解析式为y=kx+t,
∵B(4,0),E(-2,-3),
∴![]() ,
,
解得k=![]() ,b=-2.
,b=-2.
∴直线BE的解析式为y=![]() x-2.
x-2.
(2)当x=0时,y=![]() x-2=-2.
x-2=-2.
∴C的坐标是(0,-2)
如图,当点F在点C上方时,
∵△DCF≌△OCB,
∴CD=OC=2.
∴BC=![]() ,
,
过点D作DH⊥OB,垂足为H.
∴DH//OC,
∴![]() .
.
∴![]() .
.
∴OH=![]() .
.
把x=![]() 代入y=
代入y=![]() x-2得,y=
x-2得,y=![]() .
.
∴点D的坐标为(![]() ,
,![]() ).
).
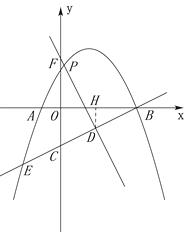
如图,当点F在点C下方时,
∵△DCF≌△OCB,
∴CD=OC=2.
过点D作DH⊥OF,垂足为H.
∴DH//OC,
∴![]() .
.
∴![]() .
.
∴DH=![]()
把x=![]() 代入y=
代入y=![]() x-2得,y=
x-2得,y=![]() .
.
∴点D的坐标为(![]() ,
,![]() ).
).
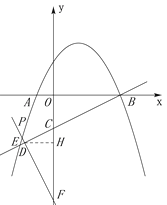
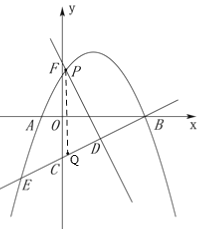
(3)①如图,过点P作PQ//FC,交BE于Q,
∴∠OCB=∠PQD,
∵sin∠PQD=sin∠OCB=![]() =
=![]() ,
,
∵点P横坐标为m,
∴P(m,![]() ),Q(m,
),Q(m,![]() ),
),
∴PQ=![]() -(
-(![]() )=
)=![]() ,
,
∴PD=PQ·sin∠PQD=![]() (
(![]() )=
)=![]() .
.
②∵PD=![]() =
=![]() (m-1)2+
(m-1)2+![]() ,
,
∴当m=1时,PD有最大值![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
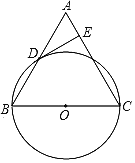
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为10,tanB=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与y轴交于点C.
(1)试用含m的代数式表示抛物线的顶点坐标;
(2)将抛物线y=x2﹣2mx+m2﹣1沿直线y=﹣1翻折,得到的新抛物线与y轴交于点D,若m>0,CD=8,求m的值.
(3)已知A(﹣k+4,1),B(1,k﹣2),在(2)的条件下,当线段AB与抛物线y=x2﹣2mx+m2﹣1只有一个公共点时,请求出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
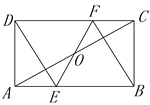
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是_______.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
查看答案和解析>>
科目:初中数学 来源: 题型:
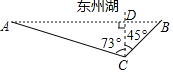
【题目】某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
科目:初中数学 来源: 题型:
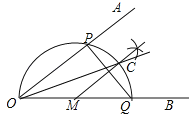
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 ![]() 于点C;
于点C;
步骤3:画射线OC.
则下列判断:①![]() =
=![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com