
【题目】如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
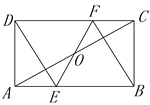
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是_______.(直接写出答案即可)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据矩形的性质可得∠OAE=∠OCF,利用ASA可证明△AOE≌△COF,可得AE=CF,即可证明BE=DF,可证明四边形DEBF是平行四边形,根据∠DFE=∠BFE及矩形性质可得∠BFE=∠BEF,即可得出BE=BF,可得四边形DEBF是菱形;
(2)如图,连接BD,由矩形的性质可得点O为BD中点,根据菱形的性质可得EF⊥BD,利用勾股定理可求出BD的长,设BE=x,则DE=x,AE=8-x,利用勾股定理可求出x的长,再利用勾股定理即可求出OE的长,进而可得EF的长.
(1)∵四边形ABCD是矩形,
∴DC∥AB,DC=AB.
∴∠OAE=∠OCF.
∵OA=OC,∠AOE=∠COF,
∴△AOE≌△COF,
∴AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵∠DFE=∠BFE,∠DFE=∠FEB,
∴∠BFE=∠BEF,
∴BE=BF,
∴四边形DEBF是菱形.
(2)如图,连接BD,
∵AB=8,AD=4,
∴BD=![]() =
=![]() ,
,
∵点C为矩形ABCD对角线AC的中点,
∴点O为BD中点,即OB=![]() BD=
BD=![]() ,
,
∵四边形DEBF是菱形,
∴EF⊥BD,EF=2OE,
设BE=x,
∵AB=8,
∴DE=BE=x,AE=8-x,
∵AD=4,
∴x2=42+(8-x)2,
解得:x=5,即BE=5,
∴OE=![]() =
=![]() ,
,
∴EF=2OE=![]() .
.


科目:初中数学 来源: 题型:
【题目】发现 对于2,4,6三个连续的偶数来说,可以得到![]() ;即前两个偶数的和等于第三个偶数;对于8,10,12,14,16五个连续的偶数来说,可以得到
;即前两个偶数的和等于第三个偶数;对于8,10,12,14,16五个连续的偶数来说,可以得到![]() ,即前三个偶数的和等于后两个偶数的和.…
,即前三个偶数的和等于后两个偶数的和.…
验证 对于九个连续偶数来说,若前五个偶数的和等于后四个偶数的和,则中间的偶数是_______;
延伸 是否存在连续的五个奇数,使得前三个奇数的和等于后两个奇数的和.若有,写出这五个奇数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图:
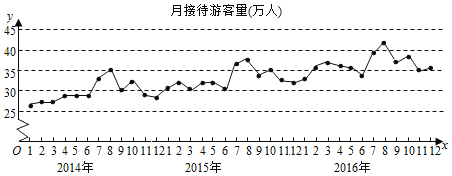
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月份
D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于直角坐标系 xOy 中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是___;
②点T在直线y=![]() x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线 y=﹣2x+2与x轴、y 轴分别交于点M、N,若线段MN上的所有点都是⊙C 的依附点,请求出圆心C的横坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:如图,二次函数![]() 经过点B(4,0)和点E(-2,-3)两点,与x轴的另一个交点为A.点D是线段BE上的动点,过点D作DF⊥BE,交y轴于点F,交抛物线于点P.
经过点B(4,0)和点E(-2,-3)两点,与x轴的另一个交点为A.点D是线段BE上的动点,过点D作DF⊥BE,交y轴于点F,交抛物线于点P.
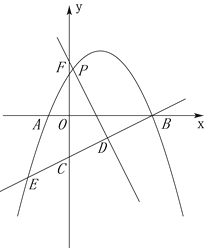
(1)求出抛物线和直线BE的解析式;
(2)当△DCF≌△BOC时,求出此时点D的坐标;
(3)设点P的横坐标为m.
①请写出线段PD的长度为(用含m的式子表示);
②当m为何值时,线段PD有最大值,并写出其最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方,原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要,公司抽调甲队外援施工,由乙队先单独施工40天后甲队返回,两队又共同施工了110天,这时甲乙两队共完成土方量103.2万立方.
(1)问甲、乙两队原计划平均每天的施工土方量分别为多少万立方?
(2)在抽调甲队外援施工的情况下,为了保证150天完成任务,公司为乙队新购进了一批机械来提高效率,那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
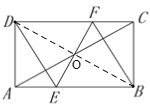
【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
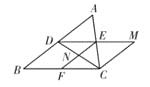
A.3对B.4对C.5对D.6对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com