
【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
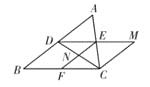
A.3对B.4对C.5对D.6对
【答案】C
【解析】
利用已知条件可证得DE,EF都是△ABC的中位线,同时可证得AE=EC,CF=![]() BC,利用三角形中位线定理可得到DE=
BC,利用三角形中位线定理可得到DE=![]() BC,DE∥BC,EF∥AB,从而可以推出∠EDC=∠FCN,DE=CF,再利用AAS证明△DEN≌△CFN,然后利用有两组对边平行的四边形是平行四边形,可证得四边形EFCM是平行四边形,再利用平行四边形的性质可以推出△EMC≌△CFE,△ADE≌△CME,△ADE≌△CEF, △BCD≌△MDC.
BC,DE∥BC,EF∥AB,从而可以推出∠EDC=∠FCN,DE=CF,再利用AAS证明△DEN≌△CFN,然后利用有两组对边平行的四边形是平行四边形,可证得四边形EFCM是平行四边形,再利用平行四边形的性质可以推出△EMC≌△CFE,△ADE≌△CME,△ADE≌△CEF, △BCD≌△MDC.
证明:∵D,E,F分别是AB,AC,BC边的中点.
∴CF=![]() BC,DE是△ABC的中位线,EF是△ABC的中位线,AE=EC
BC,DE是△ABC的中位线,EF是△ABC的中位线,AE=EC
∴DE=![]() BC,DE∥BC,EF∥AB,
BC,DE∥BC,EF∥AB,
∴∠EDC=∠FCN,DE=CF
在△DEN和△CFN中
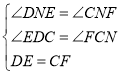
∴△DEN≌△CFN(AAS);
∵EF∥AB,CM∥AB
∴EF∥CM,DE∥BC
∴四边形EFCM是平行四边形,
∴EM=CF=DE,EF=CM,
在△EMC和△CFE中,
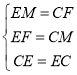
∴△EMC≌△CFE(SSS);
在△ADE和△CME中,

∴△ADE≌△CME(SAS);
∴△ADE≌△CEF,
∴DE∥BC
又BD∥CM∥EF
∴四边形DBCM是平行四边形,
∴△BCD≌△MDC
∴图中的全等三角形一共有5对.
故答案为:C.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
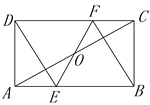
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是_______.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,当⊙G最小时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
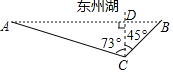
【题目】某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
科目:初中数学 来源: 题型:
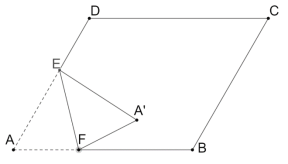
【题目】如图,在菱形![]() 中,
中,![]() ,
, ![]() , 点
, 点![]() 在边
在边![]() 上,且
上,且![]() ,点
,点![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),将菱形沿直线
重合),将菱形沿直线![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,当
,当![]() 落在菱形的对角线上时,
落在菱形的对角线上时,![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,![]() ,
,![]() 是
是![]() 的中线,
的中线,![]() ,垂足为
,垂足为![]() .像
.像![]() 这样的三角形均为“中垂三角形”.设
这样的三角形均为“中垂三角形”.设![]() ,
,![]() ,
,![]() .
.
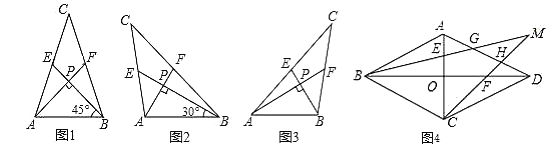
特例探索:
(1)①如图1,当![]() ,
,![]() 时,
时,![]() _________,
_________,![]() ________;
________;
②如图2,当![]() ,
,![]() 时,求
时,求![]() 和
和![]() 的值.
的值.
归纳证明:
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)利用(2)中的结论,解答下列问题:在边长为3的菱形![]() 中,
中,![]() 为对角线
为对角线![]() ,
,![]() 的交点,
的交点,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 并延长交于点
并延长交于点![]() ,
,![]() ,
,![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() ,如图4所示,求
,如图4所示,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com