
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,![]() ,
,![]() 是
是![]() 的中线,
的中线,![]() ,垂足为
,垂足为![]() .像
.像![]() 这样的三角形均为“中垂三角形”.设
这样的三角形均为“中垂三角形”.设![]() ,
,![]() ,
,![]() .
.
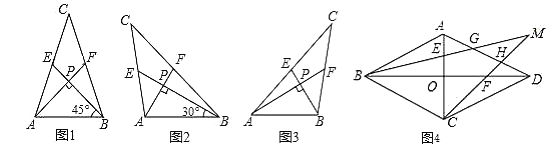
特例探索:
(1)①如图1,当![]() ,
,![]() 时,
时,![]() _________,
_________,![]() ________;
________;
②如图2,当![]() ,
,![]() 时,求
时,求![]() 和
和![]() 的值.
的值.
归纳证明:
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)利用(2)中的结论,解答下列问题:在边长为3的菱形![]() 中,
中,![]() 为对角线
为对角线![]() ,
,![]() 的交点,
的交点,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 并延长交于点
并延长交于点![]() ,
,![]() ,
,![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() ,如图4所示,求
,如图4所示,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
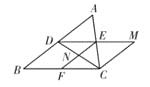
A.3对B.4对C.5对D.6对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,将![]() 放置在第一象限,且
放置在第一象限,且![]() 轴,直线
轴,直线![]() 从原点出发沿
从原点出发沿![]() 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度
轴正方向平移,在平移过程中直线被平行四边形截得的线段长度![]() 与直线在
与直线在![]() 轴上平移的距离
轴上平移的距离![]() 的函数图象如图2所示,则平行四边形
的函数图象如图2所示,则平行四边形![]() 的面积为___________.
的面积为___________.
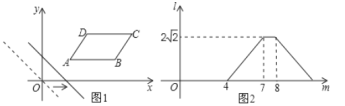
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的网民们关注的热点话题分别有:消费、教育、环保、反腐、及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2所示,请根据图中信息解答下列问题.
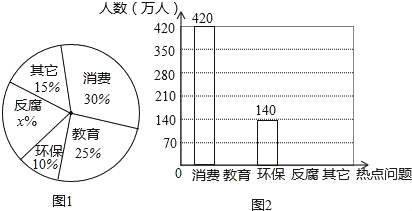
(1)求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)为了深入探讨政府工作报告,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表,请你用列表法或画树状图的方法,求出一次所选代表恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
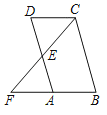
【题目】如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)求证:△CDE∽△FAE;
(2)当E是AD的中点且BC=2CD时,直接写出图中所有与∠F相等的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com