
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A�������ǣ�4��0��������OA��OC��4OB������P�ڹ�A��B��C������������ϣ�
��1���������ߵĽ���ʽ��
��2���Ƿ���ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱ��y���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF���е�GΪԲ�ģ���EFΪֱ������G������G��Сʱ�������P�����꣮

���𰸡���1��y����x2+3x+4����2�����ڣ�P�������ǣ�2��6����2����6������3�� ��
��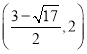
��������
��1�����ȸ�������ó�C��B�����꣬�����ô���ϵ����������κ�������ʽ���ɣ�
��2���ֱ����õ�һ�����������CΪֱ�Ƕ���ʱ���ڶ������������AΪֱ�Ƕ���ʱ���ó�P�����꼴�ɣ�
��3�����ݴ��߶���̣��ɵõ�OD��ACʱ��OD��̣���EF��̣������ó�P�����꼴�ɣ�
�⣺��1����A��4��0������֪OA��4��
��OA��OC��4OB��
��OA��OC��4��OB��1��
��C��0��4����B����1��0����
�������ߵĽ���ʽ��y��ax2+bx+c��
�� ��
��
��ã�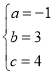 ��
��
�������ߵĽ���ʽ�ǣ�y����x2+3x+4��
��2�����ڣ�
��һ���������ͼ1������CΪֱ�Ƕ���ʱ������C��CP1��AC�����������ڵ�P1��
����P1��y��Ĵ��ߣ�������M��
�ߡ�ACP1��90����
���MCP1+��ACO��90����
�ߡ�ACO+��OAC��90����
���MCP1����OAC��
��OA��OC��
���MCP1����OAC��45����
���MCP1����MP1C��
��MC��MP1��
��P��m����m2+3m+4������m����m2+3m+4��4��
��ã�m1��0����ȥ����m2��2��
����m2+3m+4��6��
��P��2��6����
�ڶ����������ͼ1������AΪֱ�Ƕ���ʱ����A��AP2��AC���������ڵ�P2��
����P2��y��Ĵ��ߣ�������N��AP��y���ڵ�F��
��P2N��x�ᣬ
����CAO��45����
���OAP��45����
���FP2N��45����AO��OF��
��P2N��NF��
��P2��n����n2+3n+4������n������n2+3n+4��+4��
��ã�n1����2��n2��4����ȥ����
����n2+3n+4����6��
��P2�������ǣ���2����6����
����������P�������ǣ�2��6����2����6����
��3����ͼ2������OD���������֪���ı���OFDE�Ǿ��Σ���OD��EF��
���ݴ��߶���̣��ɵõ�OD��ACʱ��OD��̣���EF��̣�
�ɣ�1����֪����ֱ����AOC�У�OC��OA��4��
��AC��![]() ��4
��4![]() ��
��
���ݵ��������ε����ʣ�D��AC���е㣮
����DF��OC��
��DF��![]() OC��2��
OC��2��
����P����������2��
��x2+3x+4��2��
��ã�x��![]() ��
��
����EF���ʱ��Բ��С����P�������ǣ� ��
��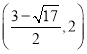 ��
��





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ཻ��
�ཻ��![]() ����ֱ��
����ֱ��![]() �Ϸֱ�ȡ��
�Ϸֱ�ȡ��![]() ,ʹ
,ʹ![]() ���ֱ����A��B��ֱ��
���ֱ����A��B��ֱ��![]() �Ĵ��ߣ�����ֱ�Ϊ
�Ĵ��ߣ�����ֱ�Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ����
����![]() ����
����![]() ��
��
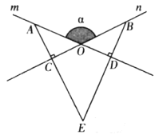
��1����֤��![]() ��
��
��2��С��˵������![]() ����ǻ��Ƕ۽ǣ���
����ǻ��Ƕ۽ǣ���![]() ����
����![]() ��ƽ�����ϣ�����Ϊ��˵���е����𣿲�˵�����ɣ�
��ƽ�����ϣ�����Ϊ��˵���е����𣿲�˵�����ɣ�
��3������![]() ����
����![]() �����ǰ����״��ͬʱ��ֱ��д��
�����ǰ����״��ͬʱ��ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ������ϵ xOy �еĵ�P�͡�C���������¶��壺����C�ϴ���������A��B��ʹ�õ�P������BC�ϣ��ҡ�APB��![]() ��ACB��0������ACB��180���������PΪ��C�������㣮
��ACB��0������ACB��180���������PΪ��C�������㣮
��1������O�İ뾶Ϊ1ʱ
����֪��D����1��0����E��0����2����F��2.5��0�����ڵ�D��E��F�У���O����������___��
����T��ֱ��y=![]() x�ϣ���TΪ��O�������㣬���T�ĺ�����t��ȡֵ��Χ��
x�ϣ���TΪ��O�������㣬���T�ĺ�����t��ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ�� y����2x+2��x�ᡢy ��ֱ��ڵ�M��N�����߶�MN�ϵ����е㶼�ǡ�C �������㣬�����Բ��C�ĺ�����n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������еĴ��·�����е�һ���ص���������.ij���̹�˾�н���һ��·�����̵�ʩ��������Ϊ120��������ԭ�ƻ��ɹ�˾�ļס����������̶Ӵӹ�·������ͬʱ����ʩ��150�����.�������������Ҫ����˾�������Ԯʩ�������Ҷ��ȵ���ʩ��40���ӷ��أ������ֹ�ͬʩ����110�죬��ʱ�������ӹ����������103.2������.
��1���ʼס�������ԭ�ƻ�ƽ��ÿ���ʩ���������ֱ�Ϊ������������
��2���ڳ������Ԯʩ��������£�Ϊ�˱�֤150���������˾Ϊ�Ҷ��¹�����һ����е�����Ч�ʣ���ô�Ҷ�ƽ��ÿ���ʩ������������Ҫ��ԭ����߶������������ܱ�֤��ʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
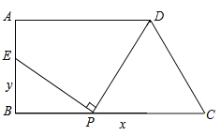
����Ŀ����ͼ������ABCD�У�AD��BC����ABC=90�㣬AD=9��BC=12��AB=6�����߶�BC����ȡһ��P������DP��������PE��DP��PE��ֱ��AB���ڵ�E.
��1����ȷ����CP=3ʱ����E��λ�ã�
��2������CP=x��BE=y����д��y�����Ա���x�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ����������ȵ���ABC�У� D��E��F�ֱ���AB��AC��BC�ߵ��е㣮����DE������C��CM��AB��DE���ӳ����ڵ�M������CD��EF���ڵ�N����ͼ��ȫ�������ι��У� ��
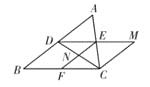
A.3��B.4��C.5��D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ���ϡ��ȿ����¼��ĸ��ʡ���ڿ�ʱ����ͬѧ�������һ�����⣺�����ͬʱ���Ͷ����ö�ʵؾ��ȵ����ӣ����dz���һ��ĵ������Ƕ��ٵĿ��������ͬѧ��չ�����ۣ����㼺��������С����С����λͬѧ���������ֲ�ͬ�Ļش�С����Ϊ6�Ŀ��������С����Ϊ7�Ŀ������������Ϊ�������Ļش���ȷ�������б�����״ͼ�ȷ�������˵���������ӣ��������Ϸֱ����1��2��3��4��5��6��СԲ���С�����壮��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���![]() �����ڵ�һ���ޣ���
�����ڵ�һ���ޣ���![]() �ᣬֱ��
�ᣬֱ��![]() ��ԭ�������
��ԭ�������![]() ��������ƽ�ƣ���ƽ�ƹ�����ֱ�߱�ƽ���ı��νصõ��߶γ���
��������ƽ�ƣ���ƽ�ƹ�����ֱ�߱�ƽ���ı��νصõ��߶γ���![]() ��ֱ����
��ֱ����![]() ����ƽ�Ƶľ���
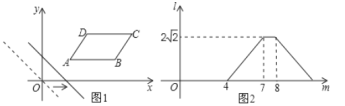
����ƽ�Ƶľ���![]() �ĺ���ͼ����ͼ2��ʾ����ƽ���ı���
�ĺ���ͼ����ͼ2��ʾ����ƽ���ı���![]() �����Ϊ___________��
�����Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CDΪ��O���ң�����AC��BD���뾶CO��BD�ڵ�E������C�����ߣ���AB���ӳ����ڵ�F���ҡ�CFA����DCA��

��1����֤��OE��BD��
��2����BE��4��CE��2�����O�İ뾶���� ������AC�ij����� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com