练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】孙老师在上《等可能事件的概率》这节课时，给同学们提出了一个问题：“如果同时随机投掷两枚质地均匀的骰子，它们朝上一面的点数和是多少的可能性最大？”同学们展开讨论，各抒己见，其中小芳和小超两位同学给出了两种不同的回答．小芳认为6的可能性最大，小超认为7的可能性最大．你认为他们俩的回答正确吗？请用列表或画树状图等方法加以说明．（骰子：六个面上分别刻有1，2，3，4，5，6个小圆点的小正方体．）

    【答案】小超的回答正确，图表见解析

    【解析】

    根据题意列表，再根据表中的数据可求出所有等可能的结果数及点数之和等于6和点数之和等于7的情况数，然后分别求出点数之和等于6与点数之和等于7的概率，由此可作出判断．

    列表如下

    （1，6）

    （2，6）

    （3，6）

    （4，6）

    （5，6）

    （6，6）

    （1，5）

    （2，5）

    （3，5）

    （4，5）

    （5，5）

    （6，5）

    （1，4）

    （2.4）

    （3，4）

    （4，4）

    （5.4）

    （6，4）

    （1，3）

    （2，3）

    （3，3）

    （4，3）

    （5，3）

    （6，3）

    （1，2）

    （2，2）

    （3，2）

    （4，2

    （5，2）

    （6，2）

    （1，1）

    （2，1）

    （3，1）

    （4.1）

    （5，1）

    （6，1）

    共有36种等可能的结果数，其中点数之和等于6占5种，点数之和等于7的占6种，

    ∴点数之和为6的概率为 ，点数之和为7的概率为

    故小超的回答正确．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

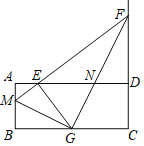
    【题目】在矩形ABCD中，AB＝4，AD＝10，E是AD的一点，且AE＝2，M是AB上一点，射线ME交CD的延长线于点F，EG⊥ME交BC于点G，连接MG，FG，FG交AD于点N．

    （1）当点M为AB中点时，则DF＝　 　，FG＝　 　．（直接写出答案）

    （2）在整个运动过程中，的值是否会变化，若不变，求出它的值；若变化，请说明理由．

    （3）若△EGN为等腰三角形时，请求出所有满足条件的AM的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

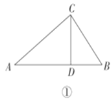
    【题目】综合与实践

    如图①，在中中，，，，过点作于，将绕点逆时针方向旋转，得到，连接，，记旋转角为．

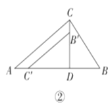
    （1）问题发现

    如图②，当时，__________；如图③，当时，__________．

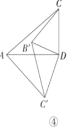
    （2）拓展探究

    试判断：当时，的大小有无变化？请仅就图④的情形给出证明．

    （3）问题解决

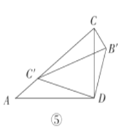
    如图⑤，当绕点逆时针旋转至点落在边上时，求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

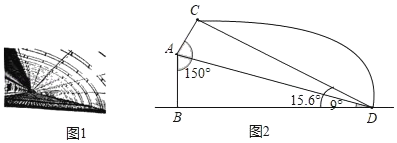
    【题目】河南省政府为促进农业发展，加快农村建设，计划扶持兴建一批新型钢管装配式大棚，如图1所示线段AB、BD分别为大棚的墙高和跨度，AC表示保温板的长，已知墙高AB为3米，墙面与保温板所成的角∠BAC＝150°，在点D处测得A点、C点的仰角分别为9°，15．6°，如图2所示求保温板AC的长是多少米？（精确到0.1米）（参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0．16，sin15.6°≈0.27，cos15.6°≈0.96，tan15.6°≈0.28，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， 在三边互不相等的△ABC中， D，E，F分别是AB，AC，BC边的中点．连接DE，过点C作CM∥AB交DE的延长线于点M，连接CD、EF交于点N，则图中全等三角形共有（ ）

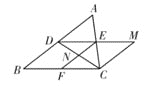
    A.3对B.4对C.5对D.6对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】张老师在讲解复习《圆》的内容时，用投影仪屏幕展示出如下内容：

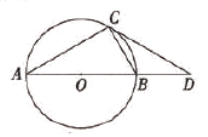
    张老师让同学们添加条件后，编制一道题目，并按要求完成下列填空．

    （1）在屏幕内容中添加条件，则的长为______．

    （2）以下是小明、小聪的对话：

    参考上面对话，在屏幕内容中添加条件，编制一道题目（此题目不解答，可以添线、添字母）．

    _________________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线与轴交于、两点，，交轴于点，对称轴是直线．

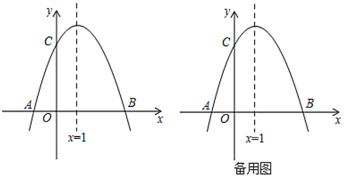
    （1）求抛物线的解析式及点的坐标；

    （2）连接，是线段上一点，关于直线的对称点正好落在上，求点的坐标；

    （3）动点从点出发，以每秒2个单位长度的速度向点运动，过作轴的垂线交抛物线于点，交线段于点．设运动时间为（）秒．若与相似，请求出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果店以10元/千克的价格购进某种水果进行销售，经过市场调查获得部分数据如下表：

    销售价格x（元/千克）

    10

    13

    16

    19

    22

    日销售量y（千克）

    100

    85

    70

    55

    40

    （1）请根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识刻画y与x之间的函数关系；

    （2）该水果店应该如何确定这批水果的销售价格，才能使日销售利润最大？

    （3）若该水果店平均每销售1千克这种水果会损耗a千克，当20≤x≤22时，水果店日获利的最大值为405元，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以点为圆心，为半径作优弧，连接，，且，在弧上任意取点(点在点的顺时针方向）且使，以为边向弧内作正三角形．

    （1）发现：不论点在弧上什么位置，点与点的距离不变，点与点的距离是_____；点到直线的最大距离是_______．

    （2）思考：当点在直线上时，求点到的距离，在备用图1中画出示意图，并写出计算过程．

    （3）探究：当与垂直或平行时，直接写出点到的距离．

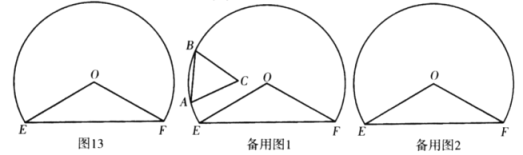
    查看答案和解析>>

    同步练习册答案