
����Ŀ��ijˮ������10Ԫ/ǧ�˵ļ۸�ij��ˮ���������ۣ������г������ò����������±���
���ۼ۸�x��Ԫ/ǧ�ˣ� | 10 | 13 | 16 | 19 | 22 |
��������y��ǧ�ˣ� | 100 | 85 | 70 | 55 | 40 |
��1������ݱ��е����ݣ�����ѧ����һ�κ��������κ�����������������֪ʶ�̻�y��x֮��ĺ�����ϵ��
��2����ˮ����Ӧ�����ȷ������ˮ�������ۼ۸���ʹ�������������
��3������ˮ����ƽ��ÿ����1ǧ������ˮ�������aǧ�ˣ���20��x��22ʱ��ˮ�����ջ��������ֵΪ405Ԫ����a��ֵ��
���𰸡���1��y����5x+150����2��������ˮ�������ۼ۸�Ϊ20Ԫ/ǧ��ʱ���������������3��a��0.2
��������
��1�����ȸ��ݱ��е����ݣ��ɲ���y��x��һ�κ�����ϵ����ѡ���������ʽ������֤�������ȷ�ԣ�
��2�����������г�����������w�����ۼ۸�x֮��ĺ�����ϵʽ�����ݶ��κ���������ȷ�����ֵ���ɣ�
��3�����������г�����������w�����ۼ۸�x֮��ĺ�����ϵʽ������������ߵĶԳ��ᣬ�ٷ���������������ۣ����ݶ��κ������������a��ֵ��
(1)ͨ���۲�����е����ݣ����ۼ۸�ÿ����3Ԫ����������y����15ǧ�ˣ�����y��x��һ�κ�����ϵ����![]() ��
��
��![]() ��
��![]() ����ã�
����ã�![]() ��
��
��ã�![]() ��
��
��![]() ��
��
���飺��![]() ��y=70����
��y=70����![]() ������һ�κ�������ʽ��
������һ�κ�������ʽ��
������ĺ�����ϵΪ![]() ��
��
(2)������������ΪWԪ��������ã�
![]()
��![]() ʱ��
ʱ��![]() ��
��
�𣺵�����ˮ�������ۼ۸�Ϊ20Ԫ/ǧ��ʱ���������������
(3) ������ã�
![]()
��Գ���Ϊֱ��![]() ��
��
����![]() ������
������![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��![]() �����
�����![]() (��ȥ)
(��ȥ)
����![]() ����
����![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��
��![]() ����ã�
����ã�![]() ��
��
���![]() (��ȥ)��
(��ȥ)��
������������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ࡱ��ʶ���������ģ�����һ��ɷ�Ϊ���ɻ���������������к��������������������м�����һ������������������������
��1��ֱ��д�������õ�����ǡ���ǡ������������ĸ��ʣ�
��2���������õ�����������ͬ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ���ϡ��ȿ����¼��ĸ��ʡ���ڿ�ʱ����ͬѧ�������һ�����⣺�����ͬʱ���Ͷ����ö�ʵؾ��ȵ����ӣ����dz���һ��ĵ������Ƕ��ٵĿ��������ͬѧ��չ�����ۣ����㼺��������С����С����λͬѧ���������ֲ�ͬ�Ļش�С����Ϊ6�Ŀ��������С����Ϊ7�Ŀ������������Ϊ�������Ļش���ȷ�������б�����״ͼ�ȷ�������˵���������ӣ��������Ϸֱ����1��2��3��4��5��6��СԲ���С�����壮��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
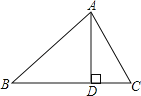
����Ŀ����ͼ������ABC�У�AD��BC��D��������������1����B+��DAC��90������2����B����DAC����3��![]() ����4��AB2��BDBC������һ���ܹ��ж���ABC��ֱ�������ε��У�����ţ�_____��
����4��AB2��BDBC������һ���ܹ��ж���ABC��ֱ�������ε��У�����ţ�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=8��BC=4����G��E�ֱ��ڱ�AB��CD�ϣ���F��H�ڶԽ���AC�ϣ����ı���EFGH�����Σ���AG�ij��ǣ� ��
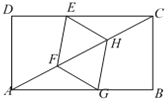
A.![]() B.5C.
B.5C.![]() D.6
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ�������̳������������̳��ķ����ǣ���һ���������������4����ȫ��ͬ��С�����Ϸֱ�ꡰ0Ԫ����20Ԫ����30Ԫ����50Ԫ�����˿�ÿ������300Ԫ�Ϳɴ������ﲻ�Żص�����2����������С��������֮�Ϳɻ���Ӧ�۸����Ʒ�����̳��ķ����ǣ���һ���������������2����ȫ��ͬ��С�����Ϸֱ�ꡰ5Ԫ����30Ԫ�����˿�ÿ������100Ԫ���Ϳɴ��������зŻص�����1������С��������ɻ���Ӧ�۸����Ʒ.ij�˿�������300Ԫ.
(1)���û���״ͼ���б���������ù˿��ڼ��̳������Ʒ���ܼ�ֵ������50Ԫ�ĸ��ʣ�
(2)�жϸù˿�ȥ�ĸ��̳�����ʹ�����Ʒ���ܼ�ֵ������50Ԫ�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
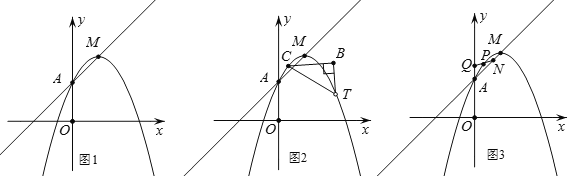
����Ŀ����ͼ1����������y=ax2(a<0)ƽ�Ƶ�����Mǡ������ֱ��y=x+3�ϣ��������߹�ֱ����y��Ľ���A�����ʱ�����߶���ĺ�����Ϊm(m>0).
(1)�ú�m�Ĵ���ʽ��ʾa��
(2)��ͼ2��Rt��CBT�������߽���C��D��T���㣬��B=90��BC��x�ᣬCD=2��BD=t��BT=2t����TDC�����Ϊ4
���������߷��̣�
����ͼ3��PΪ������AM������һ�㣬Q(0��4)������QP���ӳ����߶�AM��N����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���뷴��������
���뷴��������![]() ��ͼ���ڵ�һ�����ڵ�
��ͼ���ڵ�һ�����ڵ�![]() ������
������![]() ��
��![]() ���ϵ�
���ϵ�![]() ��
��![]() �����Ϊ
�����Ϊ![]() ��
��
��1����������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����֤��![]() �ǵ��������Σ�
�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
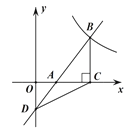
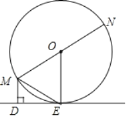
����Ŀ����֪����ͼ��MNΪ��O��ֱ����ME�ǡ�O���ң�MD��ֱ�ڹ���E��ֱ��DE������Ϊ��D����MEƽ�֡�DMN��
��֤����1��DE�ǡ�O�����ߣ�
��2��ME2��MDMN��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com