练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一次函数的图象与轴交于点，与反比例函数的图象在第一象限交于点，过点作轴上点，的面积为．

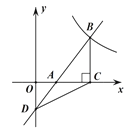
    （1）求反比例函数的解析式；

    （2）求证：是等腰三角形．

    【答案】（1）；（2）证明见解析．

    【解析】

    （1）先根据点A、B的坐标求出AC的长，再根据三角形的面积公式可求出OD的长，从而可得点D的坐标，然后利用待定系数法可求出一次函数的解析式，从而可得点B的坐标，最后利用待定系数法即可得；

    （2）先根据点B的坐标可得BC的长，再根据勾股定理可求出CD的长，从而可得，然后根据等腰三角形的定义即可得证．

    （1）∵点，点

    ∴点坐标为

    ∴

    ∴

    ∴

    ∴

    ∴点坐标为

    把，代入得：

    解得

    ∴直线的解析式为

    把点代入得

    ∴

    ∴

    则反比例函数的解析式为；

    （2）∵，，

    ∴，，

    在中，

    ∴

    ∴是等腰三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

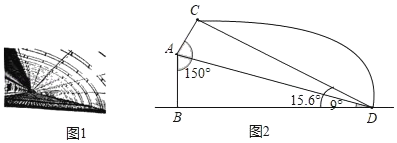
    【题目】河南省政府为促进农业发展，加快农村建设，计划扶持兴建一批新型钢管装配式大棚，如图1所示线段AB、BD分别为大棚的墙高和跨度，AC表示保温板的长，已知墙高AB为3米，墙面与保温板所成的角∠BAC＝150°，在点D处测得A点、C点的仰角分别为9°，15．6°，如图2所示求保温板AC的长是多少米？（精确到0.1米）（参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0．16，sin15.6°≈0.27，cos15.6°≈0.96，tan15.6°≈0.28，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果店以10元/千克的价格购进某种水果进行销售，经过市场调查获得部分数据如下表：

    销售价格x（元/千克）

    10

    13

    16

    19

    22

    日销售量y（千克）

    100

    85

    70

    55

    40

    （1）请根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识刻画y与x之间的函数关系；

    （2）该水果店应该如何确定这批水果的销售价格，才能使日销售利润最大？

    （3）若该水果店平均每销售1千克这种水果会损耗a千克，当20≤x≤22时，水果店日获利的最大值为405元，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

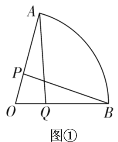
    【题目】在扇形中，，半径，点P为上任一点（不与A、O重合）.

    （1）如图①，Q是上一点，若，求证：.

    （2）如图②，将扇形沿折叠，得到O的对称点.

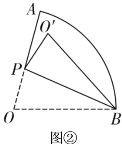
    ①若点落在上，求的长；

    ②当与扇形所在的圆相切时，求折痕的长.（注：本题结果不取近似值）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件，每件文化衫的批发价及手绘后的零售价如表：

    批发价(元)

    零售价(元)

    黑 色 文化衫

    25

    45

    白 色 文 化 衫

    20

    35

    (1)学校购进黑.白文化衫各几件？

    (2)通过手绘设计后全部售出，求该校这次义卖活动所获利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正六边形和正五边形的边重合，的延长线与交于点，则的度数是（　　 ）

    A.141B.144C.147D.150

    查看答案和解析>>

    科目：初中数学 来源： 题型：

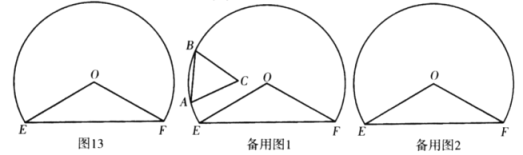
    【题目】如图，以点为圆心，为半径作优弧，连接，，且，在弧上任意取点(点在点的顺时针方向）且使，以为边向弧内作正三角形．

    （1）发现：不论点在弧上什么位置，点与点的距离不变，点与点的距离是_____；点到直线的最大距离是_______．

    （2）思考：当点在直线上时，求点到的距离，在备用图1中画出示意图，并写出计算过程．

    （3）探究：当与垂直或平行时，直接写出点到的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

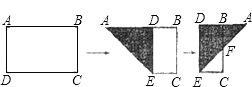
    【题目】如图，有一块矩形纸片ABCD，AB=8，AD=6．将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

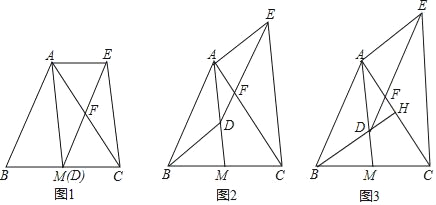
    【题目】如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）．DE∥AB交AC于点F，CE∥AM，连结AE．

    （1）如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；

    （2）如图2，当点D不与M重合时，（1）中的结论还成立吗？请说明理由．

    （3）如图3，延长BD交AC于点H，若BH⊥AC，且BH=AM．

    ①求∠CAM的度数；

    ②当FH=，DM=4时，求DH的长．

    查看答案和解析>>

    同步练习册答案