
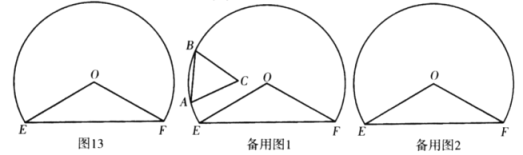
【题目】如图,以点![]() 为圆心,
为圆心,![]() 为半径作优弧
为半径作优弧![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() ,在弧
,在弧![]() 上任意取点
上任意取点![]() (点
(点![]() 在点
在点![]() 的顺时针方向)且使
的顺时针方向)且使![]() ,以
,以![]() 为边向弧内作正三角形
为边向弧内作正三角形![]() .
.
(1)发现:不论点![]() 在弧上什么位置,点
在弧上什么位置,点![]() 与点
与点![]() 的距离不变,点
的距离不变,点![]() 与点
与点![]() 的距离是_____;点
的距离是_____;点![]() 到直线
到直线![]() 的最大距离是_______.
的最大距离是_______.
(2)思考:当点![]() 在直线
在直线![]() 上时,求点
上时,求点![]() 到
到![]() 的距离,在备用图1中画出示意图,并写出计算过程.
的距离,在备用图1中画出示意图,并写出计算过程.
(3)探究:当![]() 与
与![]() 垂直或平行时,直接写出点
垂直或平行时,直接写出点![]() 到
到![]() 的距离.
的距离.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;画出示意图见解析;(3)
;画出示意图见解析;(3)![]()
【解析】
(1)根据垂直平分线的判定可证得CO垂直平分AB,再利用勾股定理分别求得OG、CG的长,进而可得OC长,如图2,当CO⊥EF时,点![]() 到直线
到直线![]() 的距离最大,利用60的正弦值可求得OH的长,进而求得EF的最大值;
的距离最大,利用60的正弦值可求得OH的长,进而求得EF的最大值;
(2)先画出示意图,然后先证![]() ∽
∽![]() ,由相似三角形的性质可求得点
,由相似三角形的性质可求得点![]() 到
到![]() 的距离;
的距离;
(3)分别画出![]() ⊥
⊥![]() 及
及![]() ∥
∥![]() 时的示意图,然后利用特殊角的三角函数值可求得点
时的示意图,然后利用特殊角的三角函数值可求得点![]() 到
到![]() 的距离.
的距离.
(1)解:如图1,连接OA、OB、OC,延长OC交AB于点G,
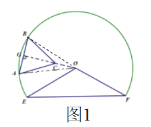
在正△ABC中,AB=BC=AC=2
∵OA=OB,AC=BC,
∴OC垂直平分AB,
∴AG=![]() AB=1,
AB=1,
∴在Rt△AGC中,CG=![]() ,
,
在Rt△AGO中,OG=![]() ,
,
∴OC=OE-CE=![]() ,
,
如图2,延长CO交EF于点H,
当CO⊥EF时,点![]() 到直线
到直线![]() 的距离最大,最大距离为CH的长,
的距离最大,最大距离为CH的长,
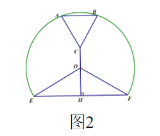
∵OE=OF,CO⊥EF,
∴CO平分∠EOF,
∵![]()
∴![]() ,
,
在Rt△EOH中,cos∠EOH=![]() ,
,
∴cos60°=![]() ,
,
∴OH=![]() ,
,
∴CH=CO+OH=![]()
∴点![]() 到直线
到直线![]() 的最大距离是
的最大距离是![]() .
.
(2)如备用图1,当点![]() 在直线
在直线![]() 时,
时,
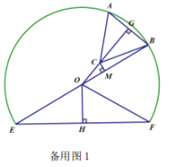
由![]() 可知,
可知,
点![]() 都在线段
都在线段![]() 的垂直平分线上,
的垂直平分线上,
![]() 过点
过点![]() 作
作![]() 的垂线垂足为
的垂线垂足为![]() ,
,
则![]() 为
为![]() 中点,直线
中点,直线![]() 过点
过点![]() .
.
由![]()
可得![]() ∽
∽![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
(3)如图3,当BC⊥OE时,设垂足为点M,
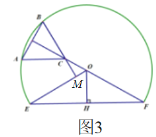
∵∠EOF=120°,
∴∠COM=180°-120°=60°,
在Rt△COM中,sin∠COM=![]() ,
,
∴sin60°=![]() ,
,
∴![]()
如图4,当BC∥OE时,过点C作CN⊥OE,垂足为点N,
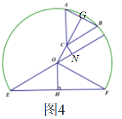
∵BC∥OE ,
∴∠CON=∠GCB=30°,
在Rt△CON中,sin∠CON=![]() ,
,
∴sin30°=![]() ,
,
∴![]() ,
,
综上所述,当![]() 与
与![]() 垂直或平行时,点
垂直或平行时,点![]() 到
到![]() 的距离为
的距离为![]() 或
或![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将抛物线y=ax2(a<0)平移到顶点M恰好落在直线y=x+3上,且抛物线过直线与y轴的交点A,设此时抛物线顶点的横坐标为m(m>0).
(1)用含m的代数式表示a;
(2)如图2,Rt△CBT与抛物线交于C、D、T三点,∠B=90,BC∥x轴,CD=2,BD=t,BT=2t,△TDC的面积为4
①求抛物线方程;
②如图3,P为抛物线AM段上任一点,Q(0,4),连结QP并延长交线段AM于N,求![]() 的最大值.
的最大值.
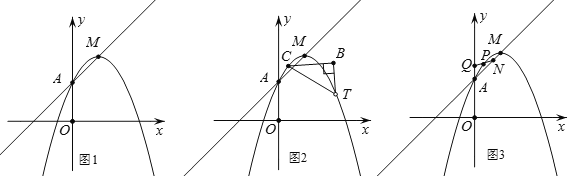
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,过点
,过点![]() 作
作![]() 轴上点
轴上点![]() ,
,![]() 的面积为
的面积为![]() .
.
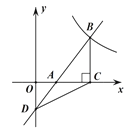
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求证:![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能够成为直角三角形三边长的三个正整数![]() 称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》,共勾股数的公式为:
称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》,共勾股数的公式为:![]() ,其中
,其中![]() 是互质的奇数.
是互质的奇数.
(1)当![]() 时,求这个三角形的面积;
时,求这个三角形的面积;
(2)当![]() 时,计算三角形的周长(用含
时,计算三角形的周长(用含![]() 的代数式表示),并直接写出符合条件的三角形的周长值.
的代数式表示),并直接写出符合条件的三角形的周长值.
查看答案和解析>>
科目:初中数学 来源: 题型:
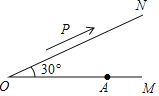
【题目】如图所示,有两条公路OM、ON相交成30°角,沿公路OM方向离O点160m处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心,100m为半径的圆形区域内都会受到卡车噪声的影响.且卡车P与学校A的距离越近,噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为15km/h.
(1)求对学校A的噪声影响最大时,卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月9日,美国政府宣布自2019年5月10日起,对中国进口的![]() 亿美元清单商品加征的关税税率由
亿美元清单商品加征的关税税率由![]() 提高到
提高到![]() .为了解我校师生对此事的关注度,学生张明采取随机抽样的方法进行问卷调查,绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: 我校师生对“加征关税税率”了解情况条形统计围我校师生对“加征关税税率”了解情况扇形统计围
.为了解我校师生对此事的关注度,学生张明采取随机抽样的方法进行问卷调查,绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: 我校师生对“加征关税税率”了解情况条形统计围我校师生对“加征关税税率”了解情况扇形统计围
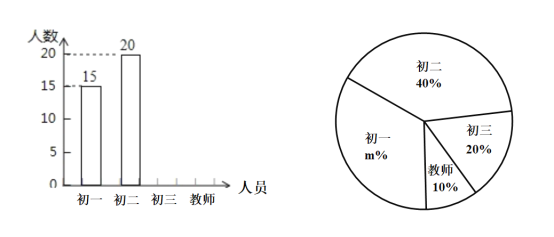
![]() 本次调查的人数有 人, 在扇形统计图中,
本次调查的人数有 人, 在扇形统计图中,![]() 的值是 ;请将条形统计图补充完整.
的值是 ;请将条形统计图补充完整.
![]() 在被调查的教师中,有
在被调查的教师中,有![]() 男
男![]() 女共
女共![]() 名教师愿意接受深入调查,现要从这
名教师愿意接受深入调查,现要从这![]() 名教师中随机抽取
名教师中随机抽取![]() 名教
名教
师进行深入调查,请画树状图或者列表求出所抽取的![]() 名教师恰好是
名教师恰好是![]() 名男教师和
名男教师和![]() 名女教师的概率.
名女教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
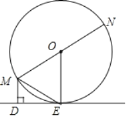
【题目】已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
求证:(1)DE是⊙O的切线;
(2)ME2=MDMN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com