
����Ŀ��2019��5��9�գ���������������2019��5��10���𣬶��й����ڵ�![]() ����Ԫ�嵥��Ʒ�����Ĺ�˰˰����
����Ԫ�嵥��Ʒ�����Ĺ�˰˰����![]() ��ߵ�
��ߵ�![]() ��Ϊ�˽���Уʦ���Դ��µĹ�ע�ȣ�ѧ��������ȡ��������ķ��������ʾ����飬����������������������ͳ��ͼ������ͼ����������Ϣ�����������: ��Уʦ������������˰˰�����˽��������ͳ��Χ��Уʦ������������˰˰�����˽��������ͳ��Χ
��Ϊ�˽���Уʦ���Դ��µĹ�ע�ȣ�ѧ��������ȡ��������ķ��������ʾ����飬����������������������ͳ��ͼ������ͼ����������Ϣ�����������: ��Уʦ������������˰˰�����˽��������ͳ��Χ��Уʦ������������˰˰�����˽��������ͳ��Χ
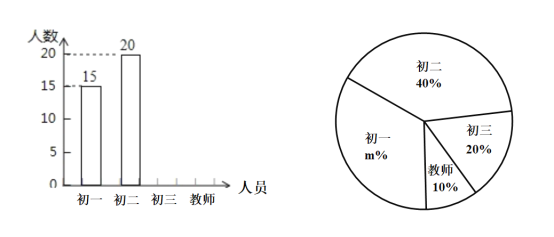
![]() ���ε���������� �ˣ� ������ͳ��ͼ�У�
���ε���������� �ˣ� ������ͳ��ͼ�У�![]() ��ֵ�� ���뽫����ͳ��ͼ����������
��ֵ�� ���뽫����ͳ��ͼ����������
![]() �ڱ�����Ľ�ʦ�У���
�ڱ�����Ľ�ʦ�У���![]() ��
��![]() ��
Ů��![]() ����ʦԸ�����������飬��Ҫ����
����ʦԸ�����������飬��Ҫ����![]() ����ʦ�������ȡ
����ʦ�������ȡ![]() ����
����
ʦ����������飬�뻭��״ͼ�����б��������ȡ��![]() ����ʦǡ����
����ʦǡ����![]() ���н�ʦ��
���н�ʦ��![]() ��Ů��ʦ�ĸ��ʣ�
��Ů��ʦ�ĸ��ʣ�
���𰸡���1��50��30������ͼ��������2��ͼ��������![]() ��
��
��������
��1�����ݳ��������Լ���ռ�ٷֱȼ���������������ó�һ����������������������ó�һ��ռ�ٷֱȣ������������Լ���������ʦ��ռ�ٷֱ�������������ɻ�������ͼ��
��2��������״ͼ�����п��ܵĽ���оٳ���������ȷ����һ��һŮ�Ŀ����м��֣����ݸ��ʵĶ�������������ɵý⣮
�⣺��1��![]() �ˣ���Ϊ
�ˣ���Ϊ![]() ������
������![]() ������������
������������![]() �ˣ���ʦ������
�ˣ���ʦ������![]() �ˣ���ȫ����ͼ����ͼ��
�ˣ���ȫ����ͼ����ͼ��
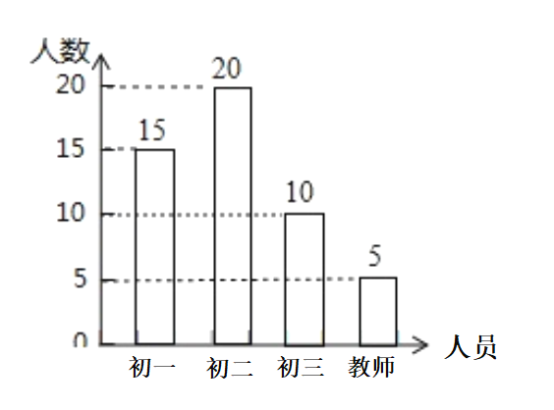
(2)��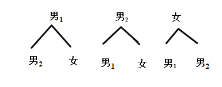
������״ͼ��֪���������ֵȿ��ܵĽ��������2����ʦǡ��1��1Ů�������ֿ���
���ʦ������������ȡ2����ʦǡ��1��1Ů�ĸ���![]() ��
��
�ʴ��ǣ���1��50��30������ͼ��������2��ͼ��������![]()


 �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д� ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬
���㣬![]() ����
����![]() ���ڵ�
���ڵ�![]() ���Գ�����ֱ��
���Գ�����ֱ��![]() ��
��
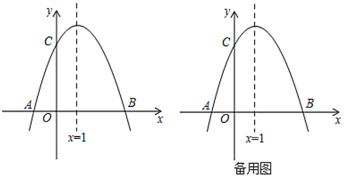
��1���������ߵĽ���ʽ����![]() �����ꣻ
�����ꣻ
��2������![]() ��
��![]() ���߶�
���߶�![]() ��һ�㣬
��һ�㣬![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��������
��������![]() �ϣ����
�ϣ����![]() �����ꣻ
�����ꣻ
��3������![]() �ӵ�
�ӵ�![]() ��������ÿ��2����λ���ȵ��ٶ����
��������ÿ��2����λ���ȵ��ٶ����![]() �˶�����
�˶�����![]() ��
��![]() ��Ĵ��߽��������ڵ�
��Ĵ��߽��������ڵ�![]() �����߶�
�����߶�![]() �ڵ�
�ڵ�![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() ��
��![]() ���룮��
���룮��![]() ��
��![]() ���ƣ������
���ƣ������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯��������С�֣������װ���������ƻ�����ڰ�������ɫ���Ļ��������ֻ���ƺ���ۣ�������������ȫ�����ɽ�����Ѻ��ӣ���֪��ѧУ�������г���4800Ԫ������ �ڰ�������ɫ���Ļ���200����ÿ���Ļ����������ۼ��ֻ������ۼ������
������(Ԫ) | ���ۼ�(Ԫ) | |
�� ɫ �Ļ��� | 25 | 45 |
�� ɫ �� �� �� | 20 | 35 |
(1)ѧУ������.���Ļ�����������
(2)ͨ���ֻ���ƺ�ȫ���۳������У����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
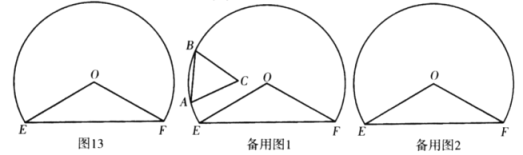
����Ŀ����ͼ���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶���Ż�
Ϊ�뾶���Ż�![]() ������
������![]() ��
��![]() ����
����![]() ���ڻ�
���ڻ�![]() ������ȡ��
������ȡ��![]() (��
(��![]() �ڵ�
�ڵ�![]() ��˳ʱ�뷽����ʹ
��˳ʱ�뷽����ʹ![]() ����
����![]() ����������������
����������������![]() ��
��
��1�����֣����۵�![]() �ڻ���ʲôλ�ã���
�ڻ���ʲôλ�ã���![]() ���
���![]() �ľ��벻�䣬��
�ľ��벻�䣬��![]() ���
���![]() �ľ�����_____����
�ľ�����_____����![]() ��ֱ��
��ֱ��![]() ����������_______��
����������_______��
��2��˼��������![]() ��ֱ��
��ֱ��![]() ��ʱ�����
��ʱ�����![]() ��
��![]() �ľ��룬�ڱ���ͼ1�л���ʾ��ͼ����д��������̣�
�ľ��룬�ڱ���ͼ1�л���ʾ��ͼ����д��������̣�
��3��̽������![]() ��
��![]() ��ֱ��ƽ��ʱ��ֱ��д����
��ֱ��ƽ��ʱ��ֱ��д����![]() ��
��![]() �ľ��룮
�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ����۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����y=��10x+500�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�������2000Ԫ����ôС��ÿ�µijɱ�������Ҫ����Ԫ�����ɱ�=��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
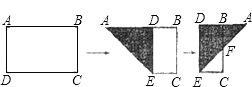
����Ŀ����ͼ����һ�����ֽƬABCD��AB=8��AD=6����ֽƬ�۵���ʹ��AD������AB���ϣ��ۺ�ΪAE���ٽ���AED��DE���ҷ��ۣ�AE��BC�Ľ���ΪF������CEF�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���е㡣������
���е㡣������![]() ������ȡһ��
������ȡһ��![]() ������
������![]() ,���߶�
,���߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת80�㣬��
��ʱ�뷽����ת80�㣬��![]() �Ķ�Ӧ���ǵ�
�Ķ�Ӧ���ǵ�![]() ������
������![]() .
.
��1����ͼ1������![]() ��������
��������![]() ��ʱ��
��ʱ��
��![]() _________________����
_________________����
��ֱ��![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ��______________________��
��λ�ù�ϵ��______________________��

��2����ͼ2������![]() ��������
��������![]() �����ʱ�����ж�ֱ��
�����ʱ�����ж�ֱ��![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ����֤����Ľ��ۡ�
��λ�ù�ϵ����֤����Ľ��ۡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬����C����O�����ߣ���ֱ��AB���ӳ��ڵ�D������ABC=65�������D�Ķ����ǣ� ��

A.25��B.30��C.40��D.50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
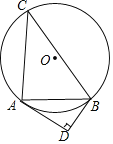
����Ŀ����ͼ����֪��O�İ뾶Ϊ5����ABC�ǡ�O���ڽ������Σ�AB��8��������B����O������BD������A��AD��BD������ΪD��
��1����֤����BAD+��C��90��
��2�����߶�AD�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com