
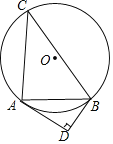
【题目】如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.
(1)求证:∠BAD+∠C=90°
(2)求线段AD的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由弦切角等于同弧所对的圆周角得:∠C=∠ABD,再根据直角三角形两锐角互余得出结论;
(2)作弦心距,由勾股定理得:OE=3,再证明△OEB∽△BDA,列比例式可以求AD的长.
:(1)∵BD为⊙O的切线,
∴∠C=∠ABD,
∵AD⊥BD,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∴∠C+∠BAD=90°,
(2)连接OB,过O作OE⊥AB于E,
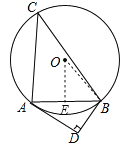
∴AE=BE=![]() AB=4,
AB=4,
由勾股定理得:OE=![]() =
=![]() =3,
=3,
∵BD为⊙O的切线,
∴OB⊥BD,
∴∠OBD=90°,
∵∠ADB=90°,
∴AD∥OB,
∴∠DAB=∠ABO,
∵∠D=∠OEB=90°,
∴△OEB∽△BDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ;
;
则线段AD的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】2019年5月9日,美国政府宣布自2019年5月10日起,对中国进口的![]() 亿美元清单商品加征的关税税率由
亿美元清单商品加征的关税税率由![]() 提高到
提高到![]() .为了解我校师生对此事的关注度,学生张明采取随机抽样的方法进行问卷调查,绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: 我校师生对“加征关税税率”了解情况条形统计围我校师生对“加征关税税率”了解情况扇形统计围
.为了解我校师生对此事的关注度,学生张明采取随机抽样的方法进行问卷调查,绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: 我校师生对“加征关税税率”了解情况条形统计围我校师生对“加征关税税率”了解情况扇形统计围
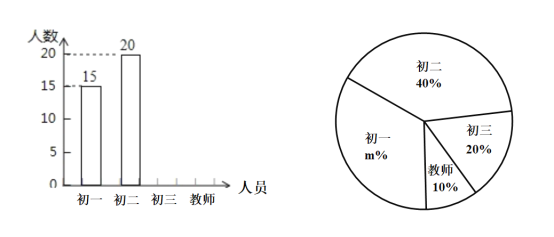
![]() 本次调查的人数有 人, 在扇形统计图中,
本次调查的人数有 人, 在扇形统计图中,![]() 的值是 ;请将条形统计图补充完整.
的值是 ;请将条形统计图补充完整.
![]() 在被调查的教师中,有
在被调查的教师中,有![]() 男
男![]() 女共
女共![]() 名教师愿意接受深入调查,现要从这
名教师愿意接受深入调查,现要从这![]() 名教师中随机抽取
名教师中随机抽取![]() 名教
名教
师进行深入调查,请画树状图或者列表求出所抽取的![]() 名教师恰好是
名教师恰好是![]() 名男教师和
名男教师和![]() 名女教师的概率.
名女教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
查看答案和解析>>
科目:初中数学 来源: 题型:
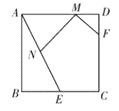
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
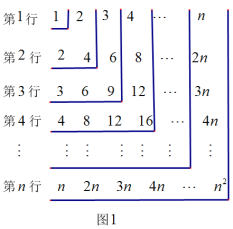
【题目】如图1,观察数表,如何计算数表中所有数的和?
方法1:如图1,先求每行数的和:
第1行 ![]()
第2行 ![]()
第n行 ![]()
故表中所有数的和:
![]() ;
;

方法2:如图2.依次以第1行每个数为起点,按顺时针方向计算各数的和:
第1组 ![]()
第2组 ![]()
第3组 ![]()
…
第![]() 组
组 ![]() ,
,
用这![]() 组数计算的结果,表示数表中所有数的和为: ,
组数计算的结果,表示数表中所有数的和为: ,
综合上面两种方法所得的结果可得等式: ;
利用上面得到的规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个三角形纸片![]() ,其中
,其中![]() ,
,![]() 分别是
分别是![]() 边上的点,连接
边上的点,连接![]() .
.
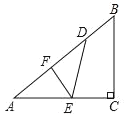
(1)如图,若将纸片![]() 的一角沿
的一角沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,且使S四边形ECBF
处,且使S四边形ECBF![]() ,求
,求![]() 的长;
的长;
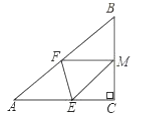
(2)如图,若将纸片![]() 的一角沿
的一角沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,且使
处,且使![]() .试判断四边形
.试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
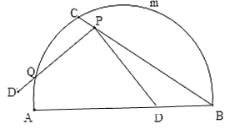
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
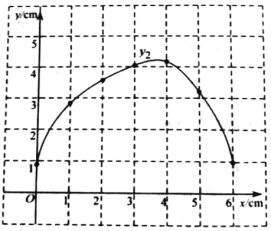
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com