
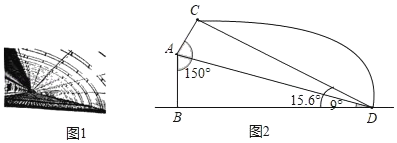
【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于![]() CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
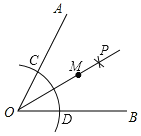
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
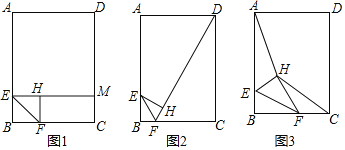
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线M:y=- ![]() x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
A.45°B.60°C.90°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC;(3)![]() ;(4)AB2=BDBC.其中一定能够判定△ABC是直角三角形的有(填序号)_____.
;(4)AB2=BDBC.其中一定能够判定△ABC是直角三角形的有(填序号)_____.
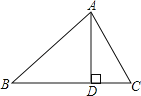
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,过点
,过点![]() 作
作![]() 轴上点
轴上点![]() ,
,![]() 的面积为
的面积为![]() .
.
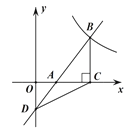
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求证:![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com