
【题目】将抛物线M:y=- ![]() x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
A.45°B.60°C.90°D.120°
【答案】C
【解析】
利用二次函数的平移规律:上加下减,左加右减,可求出抛物线M'的函数解析式,由此可得到点C的坐标,再由y=0求出抛物线M'与x轴的两个交点A,B的坐标,然后利用勾股定理求出AC2、BC2、AB2,由此可以推出AC2+BC2=AB2,利用勾股定理的逆定理,可求出∠ACB的度数.
∵y=-![]() x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M',
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M',
∴抛物线M'的解析式为y=![]()
∵ 若抛物线M'与x轴交于A、B两点,M'的顶点记为C,
∴点C(-2,3)
当y=0时![]()
解之:x1=1,x2=-5
∴点A(1,0),点B(-5,0)
∴AB2=|-5-1|2=36
AC2=32+32=18,BC2=32+32=18
∴AC2+BC2=AB2
∴∠ACB=90°.
故答案为:C.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件30元的商品,商店按单价不低于成本价,且不高于50元销售.经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
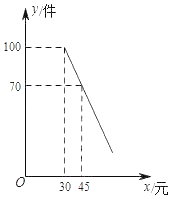
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润高于800元,请直接写出每天的销售量y(件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
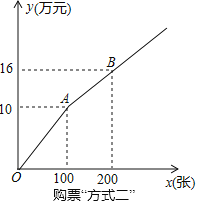
查看答案和解析>>
科目:初中数学 来源: 题型:
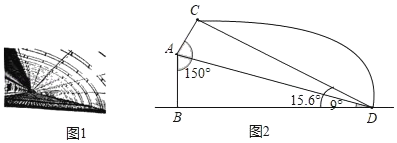
【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师在讲解复习《圆》的内容时,用投影仪屏幕展示出如下内容:
![]()
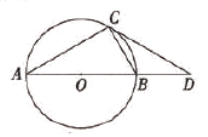
张老师让同学们添加条件后,编制一道题目,并按要求完成下列填空.
(1)在屏幕内容中添加条件![]() ,则
,则![]() 的长为______.
的长为______.
(2)以下是小明、小聪的对话:

参考上面对话,在屏幕内容中添加条件,编制一道题目(此题目不解答,可以添线、添字母).
_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
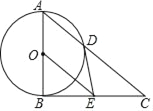
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com