
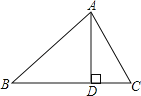
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC;(3)![]() ;(4)AB2=BDBC.其中一定能够判定△ABC是直角三角形的有(填序号)_____.
;(4)AB2=BDBC.其中一定能够判定△ABC是直角三角形的有(填序号)_____.
【答案】(2)(3)(4)
【解析】
(1)根据直角三角形中两个锐角互余,即可判定∠BAD=∠CAD,继而可得△ABC是等腰三角形,不能判定△ABC是直角三角形;
(2)利用直角三角形中两个锐角互余的知识,可得∠BAC=90°,则可得△ABC是直角三角形;
(3)由![]() ,可得
,可得![]() ,推出sin∠ACD=sin∠B,即∠ACD=∠B,由此即可判定.
,推出sin∠ACD=sin∠B,即∠ACD=∠B,由此即可判定.
(4)由AB2=BDBC与∠B是公共角,可判定△CBA∽△ABD,△ABD是直角三角形,则可得△ABC是直角三角形.
解:(1)不能,
∵AD⊥BC,
∴∠B+∠BAD=90°,
∵∠B+∠DAC=90°,
∴∠BAD=∠DAC,
∴△ABD≌△ACD(ASA),
∴AB=AC,
∴△ABC是等腰三角形,
∴无法证明△ABC是直角三角形;
(2)能,
∵AD⊥BC,
∴∠B+∠BAD=90°,
∵∠B=∠DAC,
∴∠BAC=∠BAD+∠DAC=∠BAD+∠B=90°;
(3)能,
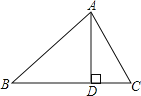
∵![]() ,
,
∴![]() ,
,
∵AD⊥BC,∴∠ADB=∠ADC=90°,
在Rt△ACD中
sin∠CAD=![]() ,
,
在Rt△ABD中,sin∠B=![]() ,
,
∴sin∠ACD=sin∠B,
∴∠ACD=∠B,
∵∠B+∠BAD=90°,
∴∠CAD+∠BAD=90°,
∴∠BAC=90°,
∴△ABC是直角三角形.
(4)能,
∵能说明△CBA∽△ABD,
又∵△ABD是直角三角形,
∴△ABC一定是直角三角形.
∴一定能够判定△ABC是直角三角形的有(2)(4)(3).
故答案为:(2)(3)(4).



 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
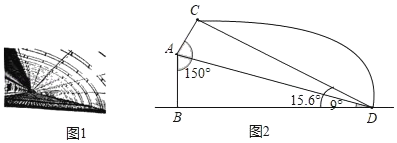
【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师在讲解复习《圆》的内容时,用投影仪屏幕展示出如下内容:
![]()
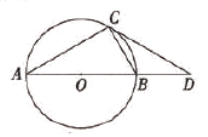
张老师让同学们添加条件后,编制一道题目,并按要求完成下列填空.
(1)在屏幕内容中添加条件![]() ,则
,则![]() 的长为______.
的长为______.
(2)以下是小明、小聪的对话:

参考上面对话,在屏幕内容中添加条件,编制一道题目(此题目不解答,可以添线、添字母).
_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
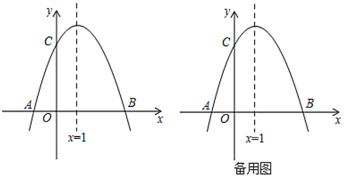
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
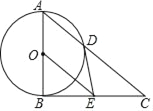
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以10元/千克的价格购进某种水果进行销售,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 10 | 13 | 16 | 19 | 22 |
日销售量y(千克) | 100 | 85 | 70 | 55 | 40 |
(1)请根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识刻画y与x之间的函数关系;
(2)该水果店应该如何确定这批水果的销售价格,才能使日销售利润最大?
(3)若该水果店平均每销售1千克这种水果会损耗a千克,当20≤x≤22时,水果店日获利的最大值为405元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
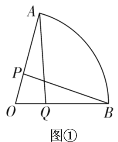
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
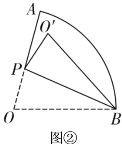
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
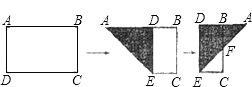
【题目】如图,有一块矩形纸片ABCD,AB=8,AD=6.将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com