
【题目】综合与实践
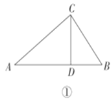
如图①,在中![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,将
,将![]() 绕点
绕点![]() 逆时针方向旋转,得到
逆时针方向旋转,得到![]() ,连接
,连接![]() ,
,![]() ,记旋转角为
,记旋转角为![]() .
.
(1)问题发现
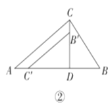
如图②,当![]() 时,
时,![]() __________;如图③,当
__________;如图③,当![]() 时,
时,![]() __________.
__________.
(2)拓展探究
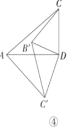
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图④的情形给出证明.
的大小有无变化?请仅就图④的情形给出证明.
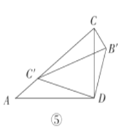
(3)问题解决
如图⑤,当![]() 绕点
绕点![]() 逆时针旋转至点
逆时针旋转至点![]() 落在边
落在边![]() 上时,求线段
上时,求线段![]() 的长.
的长.

科目:初中数学 来源: 题型:
【题目】在下面的两位数18, 27,36, 45,54,63,72,81,99都是9的整数倍,小明发现这些数的个位数字与十位数字的和也都是9的整数倍,例如18的的个位数字8与十位数字1的和是9.于是小明有了这样的结论:个位数字与十位数字的和是9的倍数的两位数一定是9的倍数.小明经过思考后给出了如下的证明:
设十位上的数字为![]() ,个位上的数字为
,个位上的数字为![]() ,并且
,并且![]() (
(![]() 为正整数)
为正整数)
那么这个两位数可表示为![]()
![]()
∴这个两位数是9的倍数
小明猜想:个位数字与十位数字与百位数字的和是9的倍数的三位数也一定是9的倍数.小明的这个猜想的结论是否正确?若正确模仿小明的证明思路给出证明,若不正确举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (
(![]() 为正整数).
为正整数).
(1)抛物线![]() 与
与![]() 轴的交点______,顶点坐标______;
轴的交点______,顶点坐标______;
(2)当![]() 时,请解答下列问题.
时,请解答下列问题.
①直接写出![]() 与
与![]() 轴的交点______,顶点坐标______,请写出抛物线
轴的交点______,顶点坐标______,请写出抛物线![]() ,
,![]() 的一条相同的图象性质______;
的一条相同的图象性质______;
②当直线![]() 与
与![]() ,
,![]() 相交共有4个交点时,求
相交共有4个交点时,求![]() 的取值范围.
的取值范围.
(3)若直线![]() (
(![]() )与抛物线
)与抛物线![]() ,抛物线
,抛物线![]() (
(![]() 为正整数)共有4个交点,从左至右依次标记为点
为正整数)共有4个交点,从左至右依次标记为点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,当
,当![]() 时,求出
时,求出![]() ,
,![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,把经过抛物线![]() (
(![]() ,
,![]() ,
, ![]() ,
,![]() 为常数)与
为常数)与![]() 轴的交点
轴的交点![]() 和顶点
和顶点![]() 的直线称为抛物线的“伴线”,若抛物线与
的直线称为抛物线的“伴线”,若抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),经过点
的右侧),经过点![]() 和点
和点![]() 的直线称为抛物线的“标线”.
的直线称为抛物线的“标线”.
(1)已知抛物线![]() ,求伴线的解析式.
,求伴线的解析式.
(2)若伴线为![]() ,标线为
,标线为![]() ,
,
①求抛物线的解析式;
②设![]() 为“标线”上一动点,过
为“标线”上一动点,过![]() 作
作![]() 平行于“伴线”,交“标线”上方的抛物线于
平行于“伴线”,交“标线”上方的抛物线于![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
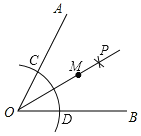
【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于![]() CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
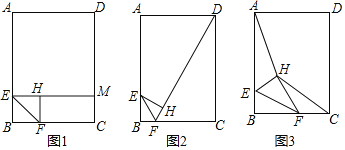
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
查看答案和解析>>
科目:初中数学 来源: 题型:
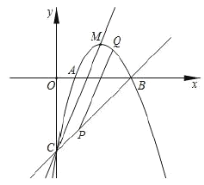
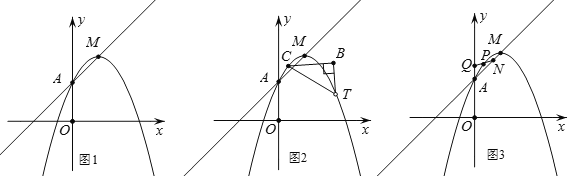
【题目】如图1,将抛物线y=ax2(a<0)平移到顶点M恰好落在直线y=x+3上,且抛物线过直线与y轴的交点A,设此时抛物线顶点的横坐标为m(m>0).
(1)用含m的代数式表示a;
(2)如图2,Rt△CBT与抛物线交于C、D、T三点,∠B=90,BC∥x轴,CD=2,BD=t,BT=2t,△TDC的面积为4
①求抛物线方程;
②如图3,P为抛物线AM段上任一点,Q(0,4),连结QP并延长交线段AM于N,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com