
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (
(![]() 为正整数).
为正整数).
(1)抛物线![]() 与
与![]() 轴的交点______,顶点坐标______;
轴的交点______,顶点坐标______;
(2)当![]() 时,请解答下列问题.
时,请解答下列问题.
①直接写出![]() 与
与![]() 轴的交点______,顶点坐标______,请写出抛物线
轴的交点______,顶点坐标______,请写出抛物线![]() ,
,![]() 的一条相同的图象性质______;
的一条相同的图象性质______;
②当直线![]() 与
与![]() ,
,![]() 相交共有4个交点时,求
相交共有4个交点时,求![]() 的取值范围.
的取值范围.
(3)若直线![]() (
(![]() )与抛物线
)与抛物线![]() ,抛物线
,抛物线![]() (
(![]() 为正整数)共有4个交点,从左至右依次标记为点
为正整数)共有4个交点,从左至右依次标记为点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,当
,当![]() 时,求出
时,求出![]() ,
,![]() 之间满足的关系式.
之间满足的关系式.
【答案】(1)![]() ,
,![]() ;
;![]() ;(2)①
;(2)①![]() ,
,![]() ;
;![]() ;对称轴为直线
;对称轴为直线![]() (或与
(或与![]() 轴交点为
轴交点为![]() ,
,![]() );②
);②![]() ,且
,且![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据![]() ,可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,本题得以解决;
,可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,本题得以解决;
(2)①将n=1,代入yn得![]() ,据此可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,然后根据(1)中的结果,写出抛物线y,yn的一条相同的图象性质即可;
,据此可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,然后根据(1)中的结果,写出抛物线y,yn的一条相同的图象性质即可;
②求出直线![]() 与
与![]() 相交只有1个交点时m的值,直线
相交只有1个交点时m的值,直线![]() 与
与![]() 相交只有1个交点时m的值,
相交只有1个交点时m的值,![]() 过点
过点![]() 时m的值,
时m的值,![]() 过点
过点![]() 时m的值,根据函数图象,从而可以得到当直线y=
时m的值,根据函数图象,从而可以得到当直线y=![]() x+m与y,yn相交共有4个交点时,m的取值范围;
x+m与y,yn相交共有4个交点时,m的取值范围;
(3)根据一元二次方程根与系数的关系求出![]() ,
,![]() ,根据
,根据![]() 可得
可得![]() ,进而可以求出k,n之间满足的关系式.
,进而可以求出k,n之间满足的关系式.
解:(1)∵抛物线![]() ,
,
∴当y=0时,x1=3,x2=1,该抛物线的顶点坐标为(1,4),
∴抛物线y=x2+2x+3与x轴的交点为(3,0),(1,0),
故答案为:(1,0),(3,0);(1,4);
(2)①当n=1时,
抛物线![]() ,
,
∴当y1=0时,x3=3,x4=1,该抛物线的顶点坐标为(1,![]() ),
),
∴该抛物线与x轴的交点为(3,0),(1,0),
抛物线y,yn的一条相同的图象性质是对称轴都是x=1(或与x轴的交点都是(1,0),(3,0));
②当直线![]() 与
与![]() 相交只有1个交点时,
相交只有1个交点时,
由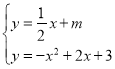 ,得
,得![]() ,
,
则![]() ,
,
∴![]() ,
,
当直线![]() 与
与![]() 相交只有1个交点时,
相交只有1个交点时,
由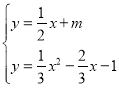 ,得
,得![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.
把![]() ,代入
,代入![]() ,得
,得![]() ;把
;把![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ;
;
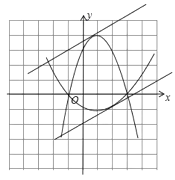
(3)由![]() ,得
,得![]() ,
,
∴![]() ,
,
由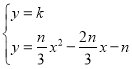 ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
化简得:![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】在证明“已知:如图,![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .”时,两位同学的证法如下:
.”时,两位同学的证法如下:
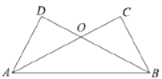
证法一:由勾股定理,得
|
证法二:
|
(1)反思:上述两位同学的证法中,有一位同学已完成的证明部分有一处错误,请把错误序号写出.
(2)请你选择其中一种证法,完成证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
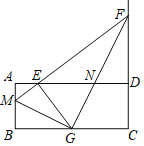
【题目】在矩形ABCD中,AB=4,AD=10,E是AD的一点,且AE=2,M是AB上一点,射线ME交CD的延长线于点F,EG⊥ME交BC于点G,连接MG,FG,FG交AD于点N.
(1)当点M为AB中点时,则DF= ,FG= .(直接写出答案)
(2)在整个运动过程中,![]() 的值是否会变化,若不变,求出它的值;若变化,请说明理由.
的值是否会变化,若不变,求出它的值;若变化,请说明理由.
(3)若△EGN为等腰三角形时,请求出所有满足条件的AM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年某省实施人才引进政策,对引进人才给予资金扶持和落户优惠,海内外英才纷纷向组织部门递交报名表.为了了解报名人员年龄结构情况,抽样调查了50名报名人员的年龄(单位:岁),将抽样得到的数据分成5组,统计如下表:
分组 | 频数(人数) | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
(1)请将表格中空格填写完整;
(2)样本数据的中位数落在_____,若把样本数据制成扇形统计图,则“大于30岁不大于40岁”的圆心角为______度;
(3)如果共有2000人报名,请你根据上面数据,估计年龄不大于40岁的报名人员会有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校共有3000人,数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
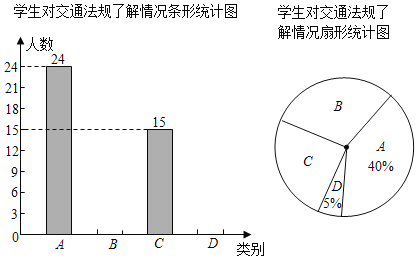
请结合图中所给的信息解答下列问题:
(1)扇形统计图中C所对应的扇形圆心角度数为 ;估计全校非常了解交通法规的有 人.
(2)补全条形统计图;
(3)学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求丙和丁两名同学同事被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图①,在中![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,将
,将![]() 绕点
绕点![]() 逆时针方向旋转,得到
逆时针方向旋转,得到![]() ,连接
,连接![]() ,
,![]() ,记旋转角为
,记旋转角为![]() .
.
(1)问题发现
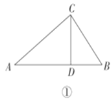
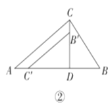
如图②,当![]() 时,
时,![]() __________;如图③,当
__________;如图③,当![]() 时,
时,![]() __________.
__________.
(2)拓展探究
试判断:当![]() 时,
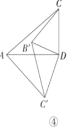
时,![]() 的大小有无变化?请仅就图④的情形给出证明.
的大小有无变化?请仅就图④的情形给出证明.
(3)问题解决
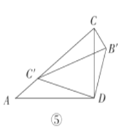
如图⑤,当![]() 绕点
绕点![]() 逆时针旋转至点
逆时针旋转至点![]() 落在边
落在边![]() 上时,求线段
上时,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
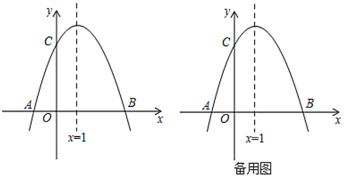
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com