
【题目】在证明“已知:如图,![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .”时,两位同学的证法如下:
.”时,两位同学的证法如下:
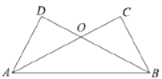
证法一:由勾股定理,得
|
证法二:
|
(1)反思:上述两位同学的证法中,有一位同学已完成的证明部分有一处错误,请把错误序号写出.
(2)请你选择其中一种证法,完成证明.
科目:初中数学 来源: 题型:
【题目】 某蛋糕店出售网红“奶昔包”,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当以40元每件出售时,每天可以卖300件,当以55元每件出售时,每天可以卖150件.
(1)求y与x之间的函数关系式;
(2)如果规定每天“奶昔包”的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该蛋糕店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试直接写出该“奶昔包”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所进行某一治疗病毒新药的开发,经过大量的服用试验后知:成年人按规定的剂量服用后,每毫克血液中含药量y微克(1微克=10-3毫克)随时间x小时的变化规律与某一个二次函数y=ax2+bx+c (a≠0)相吻合,并测得服用时(即时间为0时)每毫升血液中含药量为0微克;服用后2小时每毫升血液中含药量为6微克,服用后3小时,每毫升血液中含药量为7.5微克.
(1)求出含药量y(微克)与服药时间x(小时)的函数关系式;并画出0≤x≤8内的函数的图象的示意图;
(2)求服药后几小时才能使每毫升血液中含药量最大?并求出血液中的最大含药量;
(3)结合图象说明一次服药后的有效时间是多少小时?(有效时间为血液中含药量不为0的总时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚![]() 处测得一座建筑物顶点
处测得一座建筑物顶点![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处再测得该建筑物顶点
处再测得该建筑物顶点![]() 的仰角为
的仰角为![]() .已知
.已知![]() 米,
米,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,山坡坡度为
,山坡坡度为![]() (即
(即![]() ).注:取
).注:取![]() 为
为![]() .
.
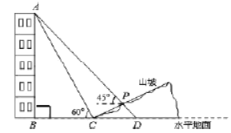
(1)求该建筑物的高度(即![]() 的长).
的长).
(2)求此人所在位置点![]() 的铅直高度(测倾器的高度忽略不计).
的铅直高度(测倾器的高度忽略不计).
(3)若某一时刻,![]() 米长木棒竖放时,在太阳光线下的水平影长是
米长木棒竖放时,在太阳光线下的水平影长是![]() 米,则同一时刻该座建筑物顶点
米,则同一时刻该座建筑物顶点![]() 投影与山坡上点
投影与山坡上点![]() 重合,求点
重合,求点![]() 到该座建筑物的水平距离.
到该座建筑物的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
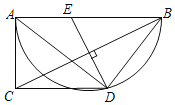
【题目】如图,AB为半圆的直径,点D在半圆弧上,过点D作AB的平行线与过点A半圆的切线交于点C,点E在AB上,若DE垂直平分BC,则![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的两位数18, 27,36, 45,54,63,72,81,99都是9的整数倍,小明发现这些数的个位数字与十位数字的和也都是9的整数倍,例如18的的个位数字8与十位数字1的和是9.于是小明有了这样的结论:个位数字与十位数字的和是9的倍数的两位数一定是9的倍数.小明经过思考后给出了如下的证明:
设十位上的数字为![]() ,个位上的数字为
,个位上的数字为![]() ,并且
,并且![]() (
(![]() 为正整数)
为正整数)
那么这个两位数可表示为![]()
![]()
∴这个两位数是9的倍数
小明猜想:个位数字与十位数字与百位数字的和是9的倍数的三位数也一定是9的倍数.小明的这个猜想的结论是否正确?若正确模仿小明的证明思路给出证明,若不正确举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (
(![]() 为正整数).
为正整数).
(1)抛物线![]() 与
与![]() 轴的交点______,顶点坐标______;
轴的交点______,顶点坐标______;
(2)当![]() 时,请解答下列问题.
时,请解答下列问题.
①直接写出![]() 与
与![]() 轴的交点______,顶点坐标______,请写出抛物线
轴的交点______,顶点坐标______,请写出抛物线![]() ,
,![]() 的一条相同的图象性质______;
的一条相同的图象性质______;
②当直线![]() 与
与![]() ,
,![]() 相交共有4个交点时,求
相交共有4个交点时,求![]() 的取值范围.
的取值范围.
(3)若直线![]() (
(![]() )与抛物线
)与抛物线![]() ,抛物线
,抛物线![]() (
(![]() 为正整数)共有4个交点,从左至右依次标记为点
为正整数)共有4个交点,从左至右依次标记为点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,当
,当![]() 时,求出
时,求出![]() ,
,![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com