
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=![]() .
.
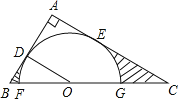
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题,材料一:定义直线y=ax+b与直线y=bx+a互为“互助直线”,例如,直线y=x+4与直y=4x+1互为“互助直线”;材料二:对于平面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2两点间的直角距离d(P1,P2)=|x1﹣x2|+|y1﹣y2|.如:Q1(﹣3,1)、Q2(2,4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8;材料三:设P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.
(1)计算S(﹣1,6),T(﹣2,3)两点间的直角距离d(S,T)= ;
(2)直线y=﹣2x+3上的一点H(a,b)又是它的“互助直线”上的点,求点H的坐标.
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“互助直线”上,试求点L(5,﹣1)到直线y=ax+b的直角距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班积极响应校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书400册.特别值得一提的是李保、王刚两位同学在父母的支持下各捐献了90册图书.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 | 4 | 5 | 6 | 7 | 8 | 90 |
人数 | 6 | 8 | 15 | 2 |
(1)分别求出该班级捐献7册图书和8册图书的人数;
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪个统计量不能反映该班同学捐书册数的一般状况,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
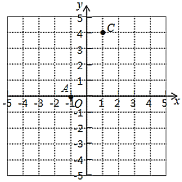
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形的面积为7?若存在,请直接写出点
三点为顶点的三角形的面积为7?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
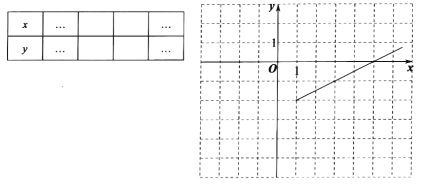
【题目】探究函数![]() 的图象和性质.静静根据学习函数的经验,对函数
的图象和性质.静静根据学习函数的经验,对函数![]() 的图象进行了探究,下面是静静的探究过程,请补充完成:
的图象进行了探究,下面是静静的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
(2)根据(1)的结果,完成下表,并补全函数![]() 图象.
图象.
(3)观察函数图象,请写出该函数的一条性质: ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com