
【题目】2018年某省实施人才引进政策,对引进人才给予资金扶持和落户优惠,海内外英才纷纷向组织部门递交报名表.为了了解报名人员年龄结构情况,抽样调查了50名报名人员的年龄(单位:岁),将抽样得到的数据分成5组,统计如下表:
分组 | 频数(人数) | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
(1)请将表格中空格填写完整;
(2)样本数据的中位数落在_____,若把样本数据制成扇形统计图,则“大于30岁不大于40岁”的圆心角为______度;
(3)如果共有2000人报名,请你根据上面数据,估计年龄不大于40岁的报名人员会有多少人?
【答案】(1)8 ,0.28 ,2 ,0.04;(2)大于30岁不大于40岁,144;(3)估计年龄不大于40岁的报名人员会有1120人.
【解析】
(1)根据频数、频率和总人数之间的关系,计算即可;
(2)根据中位数的定义判断即可;用360°乘以“大于30岁不大于40岁”的频率即可;
(3)用样本估计总体的思想计算即可.
解:(1)30岁以下的频数为:50×0.16=8,
大于40岁不大于50岁的频率为:14÷50=0.28,
60岁以上的频数为:50-8-20-14-6=2,频率为:2÷50=0.04,
填表如下:
分组 | 频数(人数) | 频率 |
30岁以下 | 8 | 0.16 |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | 0.28 |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 | 2 | 0.04 |
(2)排序后,中间两个数都在“大于30岁不大于40岁”这一组,故中位数落在“大于30岁不大于40岁”这一组;
“大于30岁不大于40岁”的圆心角为:360°×0.40=144°;
(3)![]() (人),
(人),
答:估计年龄不大于40岁的报名人员会有1120人.


科目:初中数学 来源: 题型:
【题目】某医药研究所进行某一治疗病毒新药的开发,经过大量的服用试验后知:成年人按规定的剂量服用后,每毫克血液中含药量y微克(1微克=10-3毫克)随时间x小时的变化规律与某一个二次函数y=ax2+bx+c (a≠0)相吻合,并测得服用时(即时间为0时)每毫升血液中含药量为0微克;服用后2小时每毫升血液中含药量为6微克,服用后3小时,每毫升血液中含药量为7.5微克.
(1)求出含药量y(微克)与服药时间x(小时)的函数关系式;并画出0≤x≤8内的函数的图象的示意图;
(2)求服药后几小时才能使每毫升血液中含药量最大?并求出血液中的最大含药量;
(3)结合图象说明一次服药后的有效时间是多少小时?(有效时间为血液中含药量不为0的总时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下4个项目可供选择:径赛项目:100m,200m(分别用A1、A2表示).田赛项目:跳远,跳高(分用B1,B2表示).
(1)该同学从4个项目中任选一个,恰好是田赛项目的概率为 .
(2)该同学从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率 .
查看答案和解析>>
科目:初中数学 来源: 题型:
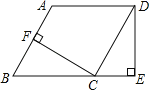
【题目】如图,在ABCD中,CF⊥AB于点F,过点D作DE⊥BC的延长线于点E,且CF=DE.
(1)求证:△BFC≌△CED;
(2)若∠B=60°,AF=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发以
点出发以![]() /秒向终点
/秒向终点![]() 运动,动点
运动,动点![]() 同时从
同时从![]() 点出发以
点出发以![]() /秒按
/秒按![]()
![]() 的方向在边
的方向在边![]() ,
,![]() ,
,![]() 上运动,设运动时间为
上运动,设运动时间为![]() (秒),那么
(秒),那么![]() 的面积
的面积![]() 随着时间
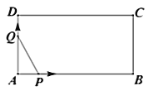
随着时间![]() (秒)变化的函数图象大致为( )
(秒)变化的函数图象大致为( )
A.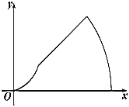 B.
B.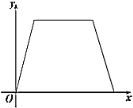 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
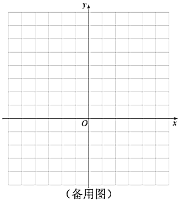
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (
(![]() 为正整数).
为正整数).
(1)抛物线![]() 与
与![]() 轴的交点______,顶点坐标______;
轴的交点______,顶点坐标______;
(2)当![]() 时,请解答下列问题.
时,请解答下列问题.
①直接写出![]() 与
与![]() 轴的交点______,顶点坐标______,请写出抛物线
轴的交点______,顶点坐标______,请写出抛物线![]() ,
,![]() 的一条相同的图象性质______;
的一条相同的图象性质______;
②当直线![]() 与
与![]() ,
,![]() 相交共有4个交点时,求
相交共有4个交点时,求![]() 的取值范围.
的取值范围.
(3)若直线![]() (
(![]() )与抛物线
)与抛物线![]() ,抛物线
,抛物线![]() (
(![]() 为正整数)共有4个交点,从左至右依次标记为点
为正整数)共有4个交点,从左至右依次标记为点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,当
,当![]() 时,求出
时,求出![]() ,
,![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
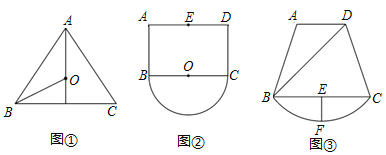
(1)如图①,在△ABC中,AB=AC=10,BC=12,点O是△ABC的外接圆的圆心,则OB的长为
问题探究
(2)如图②,已知矩形ABCD,AB=4,AD=6,点E为AD的中点,以BC为直径作半圆O,点P为半圆O上一动点,求E、P之间的最大距离;
问题解决
(3)某地有一块如图③所示的果园,果园是由四边形ABCD和弦CB与其所对的劣弧场地组成的,果园主人现要从入口D到![]() 上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,过弦BC的中点E作EF⊥BC交
米,BC=160米,过弦BC的中点E作EF⊥BC交![]() 于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,把经过抛物线![]() (
(![]() ,
,![]() ,
, ![]() ,
,![]() 为常数)与
为常数)与![]() 轴的交点
轴的交点![]() 和顶点
和顶点![]() 的直线称为抛物线的“伴线”,若抛物线与
的直线称为抛物线的“伴线”,若抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),经过点
的右侧),经过点![]() 和点
和点![]() 的直线称为抛物线的“标线”.
的直线称为抛物线的“标线”.
(1)已知抛物线![]() ,求伴线的解析式.
,求伴线的解析式.
(2)若伴线为![]() ,标线为
,标线为![]() ,
,
①求抛物线的解析式;
②设![]() 为“标线”上一动点,过
为“标线”上一动点,过![]() 作
作![]() 平行于“伴线”,交“标线”上方的抛物线于
平行于“伴线”,交“标线”上方的抛物线于![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com