
【题目】定义:如图,把经过抛物线![]() (
(![]() ,
,![]() ,
, ![]() ,
,![]() 为常数)与
为常数)与![]() 轴的交点
轴的交点![]() 和顶点
和顶点![]() 的直线称为抛物线的“伴线”,若抛物线与
的直线称为抛物线的“伴线”,若抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),经过点
的右侧),经过点![]() 和点
和点![]() 的直线称为抛物线的“标线”.
的直线称为抛物线的“标线”.
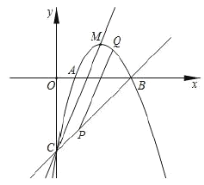
(1)已知抛物线![]() ,求伴线的解析式.
,求伴线的解析式.
(2)若伴线为![]() ,标线为
,标线为![]() ,
,
①求抛物线的解析式;
②设![]() 为“标线”上一动点,过
为“标线”上一动点,过![]() 作
作![]() 平行于“伴线”,交“标线”上方的抛物线于
平行于“伴线”,交“标线”上方的抛物线于![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 时,
时,![]() 有最大值
有最大值![]()
【解析】
(1)先根据抛物线解析式及其图象求出A、B、C、M的坐标,再根据“伴线”是过抛物线![]() (
(![]() ,
,![]() ,
, ![]() ,
,![]() 为常数)与
为常数)与![]() 轴的交点
轴的交点![]() 和顶点
和顶点![]() 的直线,可设“伴线”为
的直线,可设“伴线”为![]() ,再把点C、M代入即可求解;
,再把点C、M代入即可求解;
(2)①根据“伴线”解析式求出点C坐标,进而求出“标线”解析式和点B坐标,将点B、C代入抛物线解析式可得原抛物线的顶点式:![]() ,继而得抛物线的顶点坐标,再将抛物线顶点坐标代入伴线解析式,解方程求得a的值,继而求得抛物线解析式;
,继而得抛物线的顶点坐标,再将抛物线顶点坐标代入伴线解析式,解方程求得a的值,继而求得抛物线解析式;
②设点![]() ,根据
,根据![]() 平行于“伴线”,可设
平行于“伴线”,可设![]() 的直线解析式为
的直线解析式为![]() ,与抛物线联立可得Q点坐标,根据两点间距离公式可得PQ的长度为关于m的二次函数,根据二次函数的性质求出最大值即为PQ的最大值.
,与抛物线联立可得Q点坐标,根据两点间距离公式可得PQ的长度为关于m的二次函数,根据二次函数的性质求出最大值即为PQ的最大值.
(1) ∵![]()
令![]() ,则
,则![]() ,解得:
,解得:![]() ,
,![]()
∴![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]()
将![]() 代入抛物线解析式可得
代入抛物线解析式可得![]()
∴顶点![]() ,
,
设伴线为![]() ,把点
,把点![]() ,
,![]() 代入得:
代入得:![]()
解得:![]()
∴伴线的解析式为:![]() ;
;
(2)①伴线为![]() ,
,
令x=0,则y=﹣3,
∴![]() ,
,
∵标线为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴标线解析式为:![]() ,
,
令y=0,则x=3,
∴![]() ,
,
将点![]() ,
,![]() 代入
代入![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴抛物线顶点![]() ,
,
∴将点M代入伴线![]() ,得:
,得:![]() ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() (当
(当![]() 时,
时,![]() ,故舍去),
,故舍去),
∴抛物线解析式为:![]() ;
;
②设点![]() ,
,
∵![]() 平行于“伴线”,
平行于“伴线”,
∴![]() 的直线解析式为
的直线解析式为![]() ,
,
![]() 与抛物线的交点
与抛物线的交点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() ,即
,即![]() 时,
时,![]() 有最大值
有最大值![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
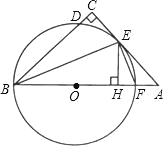
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年某省实施人才引进政策,对引进人才给予资金扶持和落户优惠,海内外英才纷纷向组织部门递交报名表.为了了解报名人员年龄结构情况,抽样调查了50名报名人员的年龄(单位:岁),将抽样得到的数据分成5组,统计如下表:
分组 | 频数(人数) | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
(1)请将表格中空格填写完整;
(2)样本数据的中位数落在_____,若把样本数据制成扇形统计图,则“大于30岁不大于40岁”的圆心角为______度;
(3)如果共有2000人报名,请你根据上面数据,估计年龄不大于40岁的报名人员会有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校共有3000人,数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
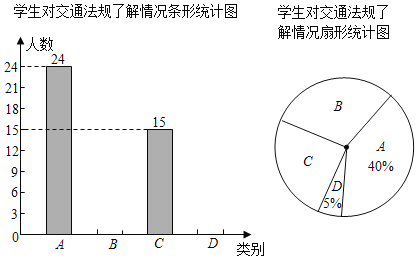
请结合图中所给的信息解答下列问题:
(1)扇形统计图中C所对应的扇形圆心角度数为 ;估计全校非常了解交通法规的有 人.
(2)补全条形统计图;
(3)学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求丙和丁两名同学同事被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的半径为1,
的半径为1,![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线
的切线![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于
于![]() 点,四边形
点,四边形![]() 是平行四边形.
是平行四边形.

(1)求![]() 的长:
的长:
(2)![]() 是
是![]() 的切线吗?若是,给出证明;若不是,说明理由.
的切线吗?若是,给出证明;若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
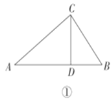
如图①,在中![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,将
,将![]() 绕点
绕点![]() 逆时针方向旋转,得到
逆时针方向旋转,得到![]() ,连接
,连接![]() ,
,![]() ,记旋转角为
,记旋转角为![]() .
.
(1)问题发现
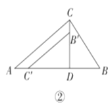
如图②,当![]() 时,
时,![]() __________;如图③,当
__________;如图③,当![]() 时,
时,![]() __________.
__________.
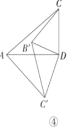
(2)拓展探究
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图④的情形给出证明.
的大小有无变化?请仅就图④的情形给出证明.
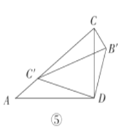
(3)问题解决
如图⑤,当![]() 绕点
绕点![]() 逆时针旋转至点
逆时针旋转至点![]() 落在边
落在边![]() 上时,求线段
上时,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
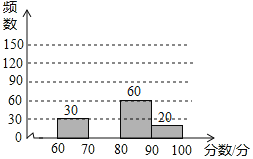
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
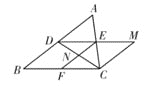
A.3对B.4对C.5对D.6对
查看答案和解析>>
科目:初中数学 来源: 题型:
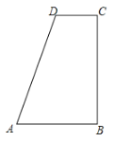
【题目】如图,在四边形ABCD中,![]() ,AB>CD,AD=AB+CD.
,AB>CD,AD=AB+CD.
(1)利用尺规作![]() ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE,EF(保留作图痕迹,不写作法);
ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE,EF(保留作图痕迹,不写作法);
(2)在(1)的条件下,证明:EC=EF;AE⊥DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com