
【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
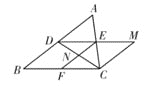
A.3对B.4对C.5对D.6对
【答案】C
【解析】
利用已知条件可证得DE,EF都是△ABC的中位线,同时可证得AE=EC,CF=![]() BC,利用三角形中位线定理可得到DE=
BC,利用三角形中位线定理可得到DE=![]() BC,DE∥BC,EF∥AB,从而可以推出∠EDC=∠FCN,DE=CF,再利用AAS证明△DEN≌△CFN,然后利用有两组对边平行的四边形是平行四边形,可证得四边形EFCM是平行四边形,再利用平行四边形的性质可以推出△EMC≌△CFE,△ADE≌△CME,△ADE≌△CEF, △BCD≌△MDC.
BC,DE∥BC,EF∥AB,从而可以推出∠EDC=∠FCN,DE=CF,再利用AAS证明△DEN≌△CFN,然后利用有两组对边平行的四边形是平行四边形,可证得四边形EFCM是平行四边形,再利用平行四边形的性质可以推出△EMC≌△CFE,△ADE≌△CME,△ADE≌△CEF, △BCD≌△MDC.
证明:∵D,E,F分别是AB,AC,BC边的中点.
∴CF=![]() BC,DE是△ABC的中位线,EF是△ABC的中位线,AE=EC
BC,DE是△ABC的中位线,EF是△ABC的中位线,AE=EC
∴DE=![]() BC,DE∥BC,EF∥AB,
BC,DE∥BC,EF∥AB,
∴∠EDC=∠FCN,DE=CF
在△DEN和△CFN中
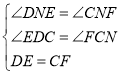
∴△DEN≌△CFN(AAS);
∵EF∥AB,CM∥AB
∴EF∥CM,DE∥BC
∴四边形EFCM是平行四边形,
∴EM=CF=DE,EF=CM,
在△EMC和△CFE中,
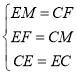
∴△EMC≌△CFE(SSS);
在△ADE和△CME中,
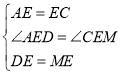
∴△ADE≌△CME(SAS);
∴△ADE≌△CEF,
∴DE∥BC
又BD∥CM∥EF
∴四边形DBCM是平行四边形,
∴△BCD≌△MDC
∴图中的全等三角形一共有5对.
故答案为:C.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
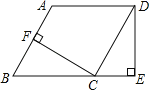
【题目】如图,在ABCD中,CF⊥AB于点F,过点D作DE⊥BC的延长线于点E,且CF=DE.
(1)求证:△BFC≌△CED;
(2)若∠B=60°,AF=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,把经过抛物线![]() (
(![]() ,
,![]() ,
, ![]() ,
,![]() 为常数)与
为常数)与![]() 轴的交点
轴的交点![]() 和顶点
和顶点![]() 的直线称为抛物线的“伴线”,若抛物线与
的直线称为抛物线的“伴线”,若抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),经过点
的右侧),经过点![]() 和点
和点![]() 的直线称为抛物线的“标线”.
的直线称为抛物线的“标线”.
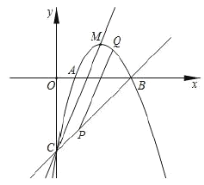
(1)已知抛物线![]() ,求伴线的解析式.
,求伴线的解析式.
(2)若伴线为![]() ,标线为
,标线为![]() ,
,
①求抛物线的解析式;
②设![]() 为“标线”上一动点,过
为“标线”上一动点,过![]() 作
作![]() 平行于“伴线”,交“标线”上方的抛物线于
平行于“伴线”,交“标线”上方的抛物线于![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
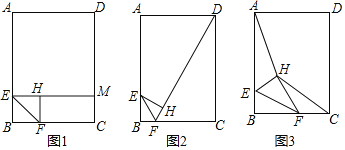
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
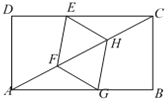
【题目】如图,矩形ABCD中,AB=8,BC=4.点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )
A.![]() B.5C.
B.5C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能够成为直角三角形三边长的三个正整数![]() 称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》,共勾股数的公式为:
称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》,共勾股数的公式为:![]() ,其中
,其中![]() 是互质的奇数.
是互质的奇数.
(1)当![]() 时,求这个三角形的面积;
时,求这个三角形的面积;
(2)当![]() 时,计算三角形的周长(用含
时,计算三角形的周长(用含![]() 的代数式表示),并直接写出符合条件的三角形的周长值.
的代数式表示),并直接写出符合条件的三角形的周长值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com