
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②P点坐标(
;②P点坐标(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,2 )(
,2 )(![]() ,2 )
,2 )
【解析】
(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式即可;
(2)作PF∥BO交AB于点F,证△PFD∽△OBD,得比例线段![]() ,则PF取最大值时,求得
,则PF取最大值时,求得![]() 的最大值;
的最大值;
(3)(i)点F在y轴上时,过点P作PH⊥x轴于H,根据正方形的性质可证明△CPH≌△FCO,根据全等三角形对应边相等可得PH=CO=2,然后利用二次函数解析式求解即可;(ii)点E在y轴上时,过点PK⊥x轴于K,作PS⊥y轴于S,同理可证得△EPS≌△CPK,可得PS=PK,则P点的横纵坐标互为相反数,可求出P点坐标;点E在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,同理可证得△PEN≌△PCM,可得PN=PM,则P点的横纵坐标相等,可求出P点坐标.
解:(1)直线y=x+4与坐标轴交于A、B两点,
当x=0时,y=4,x=﹣4时,y=0,
∴A(﹣4,0),B(0,4),
把A,B两点的坐标代入解析式得,![]() ,解得,
,解得,![]() ,
,
∴抛物线的解析式为![]() ;
;
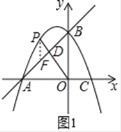
(2)①如图1,作PF∥BO交AB于点F,
∴△PFD∽△OBD,
∴![]() ,
,
∵OB为定值,
∴当PF取最大值时,![]() 有最大值,
有最大值,
设P(x,![]() ),其中﹣4<x<0,则F(x,x+4),
),其中﹣4<x<0,则F(x,x+4),
∴PF=![]() =
=![]() ,
,
∵![]() 且对称轴是直线x=﹣2,
且对称轴是直线x=﹣2,
∴当x=﹣2时,PF有最大值,
此时PF=2,![]()
![]() ;
;
②∵点C(2,0),
∴CO=2,
(i)如图2,点F在y轴上时,过点P作PH⊥x轴于H,
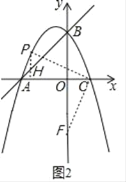
在正方形CPEF中,CP=CF,∠PCF=90°,
∵∠PCH+∠OCF=90°,∠PCH+∠HPC=90°,
∴∠HPC=∠OCF,
在△CPH和△FCO中,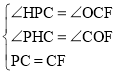 ,
,
∴△CPH≌△FCO(AAS),
∴PH=CO=2,
∴点P的纵坐标为2,
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,![]() ,
,
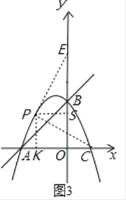
(ii)如图3,点E在y轴上时,过点PK⊥x轴于K,作PS⊥y轴于S,
同理可证得△EPS≌△CPK,
∴PS=PK,
∴P点的横纵坐标互为相反数,
∴![]() ,
,
解得x=2![]() (舍去),x=﹣2
(舍去),x=﹣2![]() ,
,
∴![]() ,
,
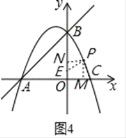
如图4,点E在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,
同理可证得△PEN≌△PCM
∴PN=PM,
∴P点的横纵坐标相等,
∴![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
综合以上可得P点坐标(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,2 )(
,2 )(![]() ,2 ).
,2 ).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
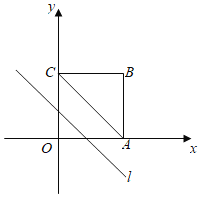
A. B.
B.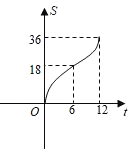
C.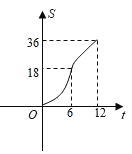 D.
D.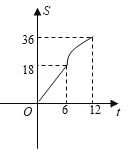
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+2与反比例函数y2=![]() 的图象交于A,B两点,点A的坐标为(1,a).
的图象交于A,B两点,点A的坐标为(1,a).
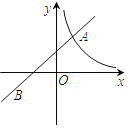
(1)求出k的值及点B的坐标;
(2)根据图象,写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与抛物线
与抛物线![]() 交于A,B两点,且点A的横坐标是
交于A,B两点,且点A的横坐标是![]() ,点B的横坐标是3,则以下结论:①抛物线
,点B的横坐标是3,则以下结论:①抛物线![]() 的图象的顶点一定是原点;②
的图象的顶点一定是原点;②![]() 时,一次函数
时,一次函数![]() 与抛物线
与抛物线![]() 的函数值都随x的增大而增大;③
的函数值都随x的增大而增大;③![]() 的长度可以等于5;④当
的长度可以等于5;④当![]() 时,
时,![]() .其中正确的结论是( )
.其中正确的结论是( )
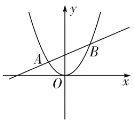
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边中点,连接
边中点,连接![]() ,点
,点![]() 为
为![]() 的中点,线段
的中点,线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() .
.
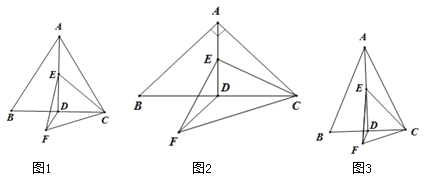
(1)如图1,当![]() 时,请直接写出
时,请直接写出![]() 的值;
的值;
(2)如图2,当![]() 时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;
时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;
(3)如图3,当![]() 时,请直接写出
时,请直接写出![]() 的值(用含
的值(用含![]() 的三角函数表示).
的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
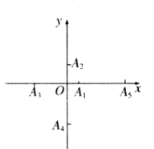
【题目】如图,在直角坐标系的坐标轴上按如下规律取点:![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() 在
在![]() 轴正半轴上,......,且
轴正半轴上,......,且![]()
![]() ......,设
......,设![]() ......,有坐标分别为
......,有坐标分别为![]() ,
,![]() ......,
......,![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,直接写出用含
时,直接写出用含![]() 为正整数)的式子表示
为正整数)的式子表示![]() 轴负半轴上所取点.
轴负半轴上所取点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月15日傍晚法国地标性建筑巴黎圣母院突遭大火吞噬,导致屋顶和主尖塔坍塌,哥特式的玫瑰花窗损毁.为了重建巴黎圣母院,设计小组设计了一个由三色玻璃拼成的花窗,如图所示,主体部分由矩形![]() 和半圆
和半圆![]() 组成,设半圆
组成,设半圆![]() 为区域
为区域![]() ,四个全等的直角三角形
,四个全等的直角三角形![]() 为区域
为区域![]() ,矩形内的阴影部分为区域
,矩形内的阴影部分为区域![]() ,其中
,其中![]() ,设
,设![]()
![]() 当
当![]() ,求区域
,求区域![]() 的面积.
的面积.
![]() 请用
请用![]() 的代数式表示出区域
的代数式表示出区域![]() 的面积并求出其最大值.
的面积并求出其最大值.
![]() 为了美观,设置区域
为了美观,设置区域![]() 与区域
与区域![]() 的面积之比为
的面积之比为![]() .区域
.区域![]() 、区域
、区域![]() 、区域
、区域![]() 分别镶嵌红、蓝、黄色三种玻璃,已知这三种玻璃的单价之和为
分别镶嵌红、蓝、黄色三种玻璃,已知这三种玻璃的单价之和为![]() 元(三种玻璃的单价均为整数),整个花窗镶嵌玻璃共花费了
元(三种玻璃的单价均为整数),整个花窗镶嵌玻璃共花费了![]() 元,求这三种玻璃的单价.(
元,求这三种玻璃的单价.(![]() 取
取![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com