
【题目】在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
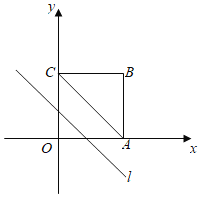
A. B.
B.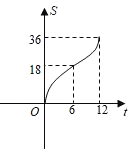
C.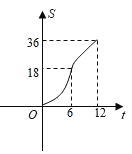 D.
D.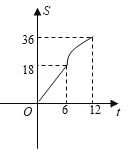
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
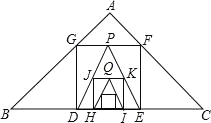
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:① ![]() ;②
;② ![]() ;③
;③ ![]() .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.
理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
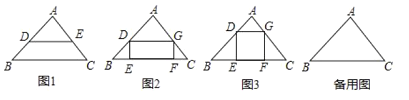
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是( )

A. CE=![]() B. EF=
B. EF=![]() C. cos∠CEP=
C. cos∠CEP=![]() D. HF2=EFCF
D. HF2=EFCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com