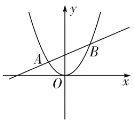
【题目】如图，一次函数
与抛物线
交于A，B两点，且点A的横坐标是
，点B的横坐标是3，则以下结论：①抛物线的图象的顶点一定是原点；②
时，一次函数与抛物线的函数值都随x的增大而增大；③
的长度可以等于5；④当
时，
.其中正确的结论是（ ）
A.①②③B.①②④C.①③④D.①②③④
【答案】B
【解析】
①由顶点坐标公式判断即可；
②根据图象得到一次函数y=kx+b为增函数，抛物线当x大于0时为增函数，本选项正确；
③AB长不可能为5，由A、B的横坐标求出AB为5时，直线AB与x轴平行，即k=0，与已知矛盾；
④直线y=-kx+b与y=kx+b关于y轴对称，作出对称后的图象，故y=-kx+b与抛物线交点横坐标分别为-3与2，找出一次函数图象在抛物线上方时x的范围判断即可．
解：①抛物线
，利用顶点坐标公式得顶点坐标为
，正确.
②由题图可知，在y轴右侧，即当
时，一次函数与抛物线的函数值都随x的增大而增大，正确.
③如解图，过点A作x轴的平行线，过点B作y轴的平行线，两线相交于点D.在
中，由A、B横坐标分别为
，3，可知
，故
，错误.
④直线
与
关于y轴对称，如解图所示，可得出直线与抛物线交点E、F横坐标分别为
，2，由解图可知当
时，
，即
，正确.
综上所述，正确的结论有①②④.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图，下面关于该班50名同学一周锻炼时间的说法错误的是（ ）
A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF．下列结论正确的是（ ）
A. CE=
B. EF=
C. cos∠CEP=
D. HF2=EFCF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，若O为BC边的中点，则必有：AB2+AC2=2AO2+2BO2成立．依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE=4，EF=3，点P在以DE为直径的半圆上运动，则PF2+PG2的最小值为（ ）
A. 
B. 
C. 34 D. 10
查看答案和解析>>
科目：初中数学 来源： 题型：
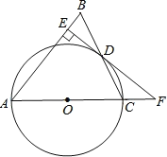
【题目】如图，在△ABC中，AB=AC，以AC边为直径作
O交BC边于点D，过点D作DE⊥AB于点E，ED、AC的延长线交于点F.
(1)求证：EF是O的切线；
(2)若EB=6，且sin∠CFD=
，求O的半径.
查看答案和解析>>
科目：初中数学 来源： 题型：
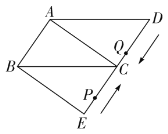
【题目】如图，在平行四边形
中，
，以B为顶点，作
交
延长线于点E.
（1）求证：四边形
是矩形；
（2）若
，
，点P从点E出发，沿
方向，以每秒1个单位的速度向终点B运动；点Q从点D出发，沿
方向，以每秒2个单位的速度向终点A运动，两点同时出发，其中一点到达终点后，另一点随之停止运动.设运动时间为
.
①若
是等腰三角形，求t的值；
②若
，直接写出t的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，直线y＝x+4与抛物线y＝﹣
x2+bx+c（b，c是常数）交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C．
（1）求该抛物线的解析式；
（2）P是抛物线上一动点（不与点A、B重合），
①如图2，若点P在直线AB上方，连接OP交AB于点D，求
的最大值；
②如图3，若点P在x轴的上方，连接PC，以PC为边作正方形CPEF，随着点P的运动，正方形的大小、位置也随之改变．当顶点E或F恰好落在y轴上，直接写出对应的点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
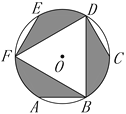
【题目】如图所示是一个圆形飞镖靶的示意图，其中A，B，C，D，E，F是⊙O的六等分点，如果向该飞镖靶上任意投一枚飞镖，则飞镖落在阴影区域的概率是_______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
