
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=3,BC=5,DE是BC的垂直平分线,DE分别交BC、AB于点D、E.
(1)求证:△ABC为直角三角形.
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<4).


(1)请在4×8的网格纸图①中画出t为3秒时的线段PQ.并求其长度;
(2)若M是BC的中点,记△PQM的面积为S,请用含有t的代数式来表示S;
(3)当t为多少时,△PQB是以PQ为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.

(1)用含t的式子表示PC的长为_______________;
(2)若点Q的运动速度与点p的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一块三角形的土地要分给甲、乙、丙三家农户. 如图,如果∠A=90°,∠B=30°.


(1)这三家农户所得土地的大小、形状都相同,请你在图中试着分一分,并简洁说明你的理由.
(2)要使这三家农户所得土地是面积相等的三角形,且有一个公共顶点,请你在备用图中试着分一分,并简洁说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行有奖促销活动,规定顾客购物达到一定金额就可以获得一次转动转盘的机会(如图),当转盘停止转动时指针落在哪一区域就可获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“10元兑换券”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“10元兑换券”的频率 | 0.68 | a | 0.68 | 0.69 | b | 0.701 |
(1)a的值为 ,b的值为 ;
(2)假如你去转动该转盘一次,获得“10元兑换券”的概率约是 ;(结果精确到0.01)
(3)根据(2)的结果,在该转盘中表示“20元兑换券”区域的扇形的圆心角大约是多少度?(结果精确到1°)

查看答案和解析>>
科目:初中数学 来源: 题型:
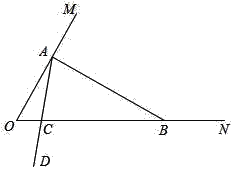
【题目】在一个钝角三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“智慧三角形”.如,三个内角分别为120°,40°,20°的三角形是“智慧三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.
(1)∠ABO的度数为_____°,△AOB_____(填“是”或“不是”) “智慧三角形”;
(2)若∠OAC=20°,求证:△AOC为“智慧三角形”;
(3)当△ABC为“智慧三角形”时,求∠OAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com