
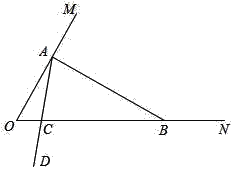
����Ŀ����һ���۽��������У����һ��������һ���ǵ�3�������������������dz�֮Ϊ���ǻ������������磬�����ڽǷֱ�Ϊ120�㣬40�㣬20���������������ǻ�������������ͼ����MON=60����������OM����һ��A������A��AB��OM��ON�ڵ�B����AΪ�˵�������AD��������OB�ڵ�C��
��1����ABO�Ķ���Ϊ_____�㣬��AOB_____���������������������� ���ǻ�����������
��2������OAC=20������֤����AOCΪ���ǻ�����������
��3������ABCΪ���ǻ���������ʱ�����OAC�Ķ�����
���𰸡���1��30���ǣ���2��֤������������3����OAC�Ķ���Ϊ80����52.5�㣮
��������
��1�����ݴ�ֱ�Ķ��塢�������ڽǺͶ��������ABO�Ķ������������ǻ����������ĸ����ж���
��2���������ǻ����������ĸ���֤��������
��3���֡�ABC=3��BAC����BCA=3��BAC����������������ǻ����������Ķ��������
��1����AB��OM�����OAB=90�㣬���ABO=90�㩁��MON=30�㣮
�ߡ�OAB=3��ABO�����AOBΪ���ǻ�����������
�ʴ�Ϊ��30������
��2����AOC=60�㣬��OAC=20�㣬���AOC=3��OAC�����AOCΪ���ǻ�����������
��3���ߡ�ABO=30�㣬���BAC+��BCA=150�㣮
�ߡ�ABCΪ���ǻ���������������ABC=3��BACʱ����BAC=10�㣬���OAC=90�㣭10��=80����
����BCA=3��BACʱ����BAC=37.5�㣬���OAC=90�㣭37.5��=52.5�㣮
����������ABCΪ���ǻ���������ʱ�����OAC�Ķ���Ϊ80����52.5�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2����2m+1��+�� ![]() m2��1����
m2��1����
��1����֤������mȡʲôʵ�����ö��κ���ͼ����x�������������㣻
��2�����ö��κ���ͼ���㣨2m��2����2m��1������ö��κ����ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��С���ƻ������ѿ��һ������Ʒ�����˽��мס������ҿ�ݹ�˾�ȽϺ��ʣ���˾��ʾ�������Ʒ������1ǧ�˵ģ���ÿǧ��22Ԫ�շѣ�����1ǧ�ˣ������IJ��ְ�ÿǧ��15Ԫ�շѣ��ҹ�˾��ʾ����ÿǧ��16Ԫ�շѣ����Ӱ�װ��3Ԫ����С�������Ʒxǧ�ˣ�
��1����ֱ�д���ס������ҿ�ݹ�˾��ݸ���Ʒ�ķ���y��Ԫ����x��ǧ�ˣ�֮��ĺ�����ϵʽ��
��2��С��ѡ���ļҿ�ݹ�˾��ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
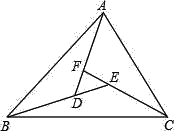
����Ŀ����ͼ����BAD=��CBE=��ACF����FDE=64�㣬��DEF=43�������ABC���ڽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC=2 ![]() ��EΪBC����һ�㣬BC=3BE��������ABCD��AE���ڵ�ֱ���۵���B��ǡ�����ڶԽ���AC�ϵ�B�䴦����AB= ��
��EΪBC����һ�㣬BC=3BE��������ABCD��AE���ڵ�ֱ���۵���B��ǡ�����ڶԽ���AC�ϵ�B�䴦����AB= ��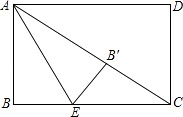
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧϰ��ʵ����ʱ����������һ��ͼ�������������ϵĵ�λ��Ϊ��1�����߶���һ�������Σ�Ȼ����ԭ��OΪԲ�ģ������εĶԽ��߳�Ϊ�뾶������x���ڵ�A���������ͼ�λش��������⣺
��1���߶�OA�ij����Ƕ��٣���Ҫ��д�������̣�
��2�����ͼ�ε�Ŀ����Ϊ��˵��ʲô��
��3�������о��ͽ������ķ�ʽ���������� ������ѧ˼�뷽�����������з��ϵ�ѡ��������ں����ϣ�
A�����ν�ϣ�B�����룻C����Ԫ��D�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㣺ab=a��1��b������a��b�Ƿ���x2��x+ ![]() m=0��m��0������������bb��aa��ֵΪ�� ��
m=0��m��0������������bb��aa��ֵΪ�� ��
A.0
B.1
C.2
D.��m�й�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����BAC=2��DAE=2����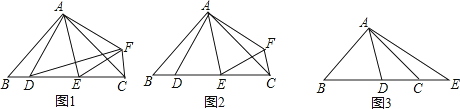
��1����ͼ1������D����ֱ��AE�ĶԳƵ�ΪF����֤����ADF�ס�ABC��
��2����ͼ2���ڣ�1���������£�����=45�㣬��֤��DE2=BD2+CE2��
��3����ͼ3������=45�㣬��E��BC���ӳ����ϣ����ʽDE2=BD2+CE2���ܳ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com