【题目】如图，∠BAD=∠CBE=∠ACF，∠FDE=64°，∠DEF=43°，求△ABC各内角的度数．
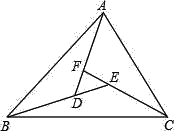
【答案】△ABC各内角的度数分别为64°、43°、73°．
【解析】
根据三角形外角性质得到∠FDE=∠BAD+∠ABD，而∠BAD=∠CBE，则∠FDE=∠BAD+∠CBE=∠ABC=64°；同理可得∠DEF=∠ACB=43°，然后根据三角形内角和定理计算∠BAC=180°﹣∠ABC﹣∠ACB即可．
∵∠FDE=∠BAD+∠ABD，∠BAD=∠CBE，∴∠FDE=∠BAD+∠CBE=∠ABC，∴∠ABC=64°；
同理：∠DEF=∠FCB+∠CBE=∠FCB+∠ACF=∠ACB，∴∠ACB=43°；
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣64°﹣43°=73°，∴△ABC各内角的度数分别为64°、43°、73°．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A（﹣1，m）和点B（n，5）．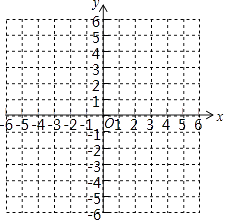 
（1）求该二次函数的关系式；
（2）在给定的平面直角坐标系中，画出这两个函数的大致图象；
（3）结合图象直接写出x2+bx+c＞x+1时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC边的中点，连接DE．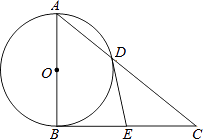 
（1）求证：DE与⊙O相切．
（2）若tanC= 
，DE=2，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC沿DE、EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO＝100°，则∠C的度数为（ ）
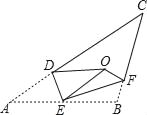
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个钝角三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“智慧三角形”．如，三个内角分别为120°，40°，20°的三角形是“智慧三角形”．如图，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交射线OB于点C．
（1）∠ABO的度数为_____°，△AOB_____（填“是”或“不是”） “智慧三角形”；
（2）若∠OAC=20°，求证：△AOC为“智慧三角形”；
（3）当△ABC为“智慧三角形”时，求∠OAC的度数．
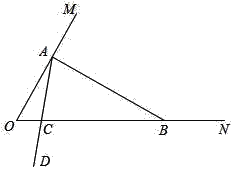
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=BC，∠ACB=90°，点D、E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A、B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C、B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是（ ）
A．90° B．120° C．135° D．150°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学数学活动小组为了调查居民的用水情况，从某社区的1500户家庭中随机抽取了30户家庭的月用水量，结果如下表所示：
月用水量（吨） | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
户 数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
（1）求这30户家庭月用水量的平均数，众数和中位数；
（2）根据上述数据，试估计该社区的月用水量；
（3）由于我国水资源缺乏，许多城市常利用分段计费的办法引导人们节约用水，即规定每个家庭的月基本用水量为m（吨），家庭月用水量不超过m（吨）的部分按原价收费，超过m吨部分加倍收费，你认为上述问题中的平均数、众数、中位数中哪一个量作为月基本用水量比较合理？简述理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某次篮球联赛初赛阶段，每队有
场比赛，每场比赛都要分出胜负，每队胜一场得
分， 负一场得
分，积分超过
分才能获得参赛资格.
（1）已知甲队在初赛阶段的积分为
分，求甲队初赛阶段胜、负各多少场；
（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
