
【题目】如图,在平行四边形![]() 中,
中,![]() ,以B为顶点,作
,以B为顶点,作![]() 交
交![]() 延长线于点E.
延长线于点E.
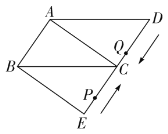
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,点P从点E出发,沿
,点P从点E出发,沿![]() 方向,以每秒1个单位的速度向终点B运动;点Q从点D出发,沿
方向,以每秒1个单位的速度向终点B运动;点Q从点D出发,沿![]() 方向,以每秒2个单位的速度向终点A运动,两点同时出发,其中一点到达终点后,另一点随之停止运动.设运动时间为
方向,以每秒2个单位的速度向终点A运动,两点同时出发,其中一点到达终点后,另一点随之停止运动.设运动时间为![]() .
.
①若![]() 是等腰三角形,求t的值;
是等腰三角形,求t的值;
②若![]() ,直接写出t的值.
,直接写出t的值.
【答案】(1)详见解析;(2)①t的值为2或0或![]() ;②
;②![]() .
.
【解析】
(1)根据有一个角是直角的平行四边形是矩形判定;
(2)①分(ⅰ)当![]() ,(ⅱ)当
,(ⅱ)当![]() ,(ⅲ)当
,(ⅲ)当![]() 三种情况,列出含t的等式,即可求出t的值;
三种情况,列出含t的等式,即可求出t的值;
②根据题意判定可得只有点P在![]() 上,点Q在
上,点Q在![]() 上时,
上时,![]() ,设PQ与BC的交点为N,证明
,设PQ与BC的交点为N,证明![]() ,得出
,得出![]() ,从而解得t值.
,从而解得t值.
(1)证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,
∴四边形![]() 是矩形;
是矩形;
(2)解:①∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() .
.
∵四边形![]() 是矩形,∴
是矩形,∴![]() .
.
若![]() 是等腰三角形,则有:
是等腰三角形,则有:
(ⅰ)当![]() ,此时有
,此时有![]() ,解得
,解得![]() ;
;
(ⅱ)当![]() ,此时有
,此时有![]() ,解得
,解得![]() ;
;
(ⅲ)当![]() 时,如解图①,过点P作
时,如解图①,过点P作![]() 于点M,则
于点M,则![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
综上,若![]() 是等腰三角形,t的值为2或0或
是等腰三角形,t的值为2或0或![]() ;
;
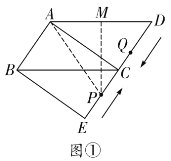

②![]() .
.
由题意可知,当![]() 时,只有点P在
时,只有点P在![]() 上,点Q在
上,点Q在![]() 上时符合题意,如解图②所示,设PQ与BC的交点为N,
上时符合题意,如解图②所示,设PQ与BC的交点为N,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
当![]() 时,点Q在
时,点Q在![]() 上,点P在
上,点P在![]() 上,此时
上,此时![]() ,
,![]() .
.
∵四边形![]() 是矩形,∴
是矩形,∴![]() .
.
当![]() 时,有
时,有![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]() .∴
.∴![]() .
.


科目:初中数学 来源: 题型:
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
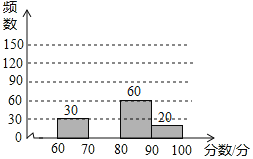
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
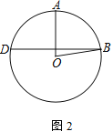
【题目】如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1) 若点C在优弧BD上,求∠ACD的大小
(2) 若点C在劣弧BD上,直接写出∠ACD的大小
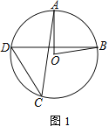
查看答案和解析>>
科目:初中数学 来源: 题型:
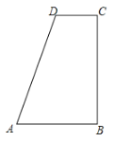
【题目】如图,在四边形ABCD中,![]() ,AB>CD,AD=AB+CD.
,AB>CD,AD=AB+CD.
(1)利用尺规作![]() ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE,EF(保留作图痕迹,不写作法);
ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE,EF(保留作图痕迹,不写作法);
(2)在(1)的条件下,证明:EC=EF;AE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与抛物线
与抛物线![]() 交于A,B两点,且点A的横坐标是
交于A,B两点,且点A的横坐标是![]() ,点B的横坐标是3,则以下结论:①抛物线
,点B的横坐标是3,则以下结论:①抛物线![]() 的图象的顶点一定是原点;②
的图象的顶点一定是原点;②![]() 时,一次函数
时,一次函数![]() 与抛物线
与抛物线![]() 的函数值都随x的增大而增大;③
的函数值都随x的增大而增大;③![]() 的长度可以等于5;④当
的长度可以等于5;④当![]() 时,
时,![]() .其中正确的结论是( )
.其中正确的结论是( )
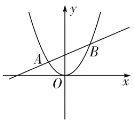
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
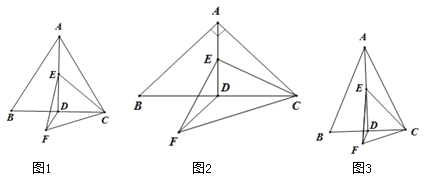
【题目】已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边中点,连接
边中点,连接![]() ,点
,点![]() 为
为![]() 的中点,线段
的中点,线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,当![]() 时,请直接写出
时,请直接写出![]() 的值;
的值;
(2)如图2,当![]() 时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;
时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;
(3)如图3,当![]() 时,请直接写出
时,请直接写出![]() 的值(用含
的值(用含![]() 的三角函数表示).
的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晋阳湖公园是华北最大的城市公园,是太原市未来的“城市客厅”,是工业文明与人文历史的交融.园内的晋阳湖是华北最大的人工湖,素称“中国北湖”.为满足晋阳湖景区水秀综合演艺的调试和表演用水需求,工程部按计划从4月1日开始向晋阳湖公园南扩湖供水,供水总量为120万立方米,经过计算,如果将原计划的每日供水量提高25%,则完成供水所需的时间将比原计划时间提前6天完成.
(1)求原计划每日的供水量与供水的天数分别是多少?
(2)工程部按原计划供水12天后,接到上级指挥部的命令,要求工程部务必与4月28日前完成供水任务.则在后一阶段的供水中,至少需将每日的供水量提高百分之多少,才能在指挥部要求的期限内完成供水任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com