
【题目】如图①,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=40°,连接BD、CE.将△ADE绕点A旋转,BD、CE也随之运动.
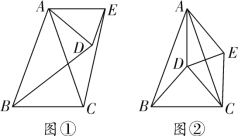
(1)求证:BD=CE;
(2)在△ADE绕点A旋转过程中,当AE∥BC时,求∠DAC的度数;
(3)如图②,当点D恰好是△ABC的外心时,连接DC,判断四边形ADCE的形状,并说明理由.
科目:初中数学 来源: 题型:
【题目】移动通信公司建设的钢架信号塔(如图1),它的一个侧面的示意图(如图2).CD是等腰三角形ABC底边上的高,分别过点A、点B作两腰的垂线段,垂足分别为B1,A1,再过A1,B1分别作两腰的垂线段所得的垂足为B2,A2,用同样的作法依次得到垂足B3,A3,….若AB为3米,sinα=![]() ,则水平钢条A2B2的长度为( )
,则水平钢条A2B2的长度为( )
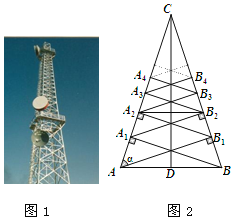
A. ![]() 米B. 2米C.
米B. 2米C. ![]() 米D.
米D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
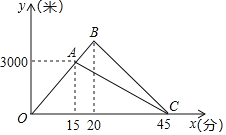
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
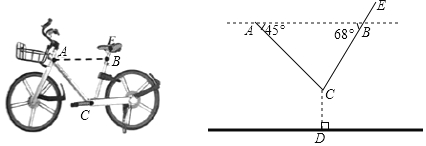
【题目】如图所示,一辆单车放在水平的地面上,车把头下方![]() 处与坐垫下方
处与坐垫下方![]() 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上,![]() ,
,![]() 之间的距离约为
之间的距离约为![]() ,现测得
,现测得![]() ,
,![]() 与
与![]() 的夹角分别为
的夹角分别为![]() 与
与![]() ,若点
,若点![]() 到地面的距离
到地面的距离![]() 为
为![]() ,坐垫中轴
,坐垫中轴![]() 处与点
处与点![]() 的距离
的距离![]() 为
为![]() ,求点
,求点![]() 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
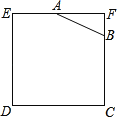
【题目】如图所示,已知边长为4的正方形钢板有一个角锈蚀,其中AF=2,BF=1,为了合理利用这块钢板.将在五边形EABCD内截取一个矩形块MDNP,使点P在AB上,且要求面积最大,求钢板的最大利用率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com