
����Ŀ����ͼ��ʾ��������y��ax2+bx+c��x�ύ��A��B���㣬A����5��0������y�ύ��C��0����5�������ҶԳ���x����3��
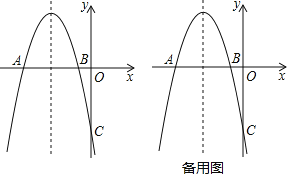
��1���������ߵĽ���ʽ��
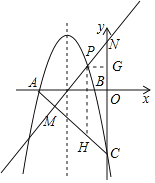
��2��P��x���Ϸ����������ϣ���P��ֱ��y��x+m��ֱ��AC���ڵ�M����y�ύ�ڵ�N����PM+MN�����ֵ��
��3����DΪ�����߶Գ�����һ�㣬
�ٵ���ACD����ACΪֱ�DZߵ�ֱ��������ʱ����D�����ꣻ
������ACD����������Σ����D���������ȡֵ��Χ��
���𰸡���1��y����x2��6x��5����2��PM+MN�����ֵΪ9![]() ����3���ٵ�D������Ϊ����3��2����3����8������D���������ȡֵ��Χ�ǩ�8��y����6��1��y��2
����3���ٵ�D������Ϊ����3��2����3����8������D���������ȡֵ��Χ�ǩ�8��y����6��1��y��2
��������
��1�����ô���ϵ�������ɵã�
��2����AC����ʽΪ![]() ����
����![]() �ᣬ��AC��H����
�ᣬ��AC��H����![]() �ᣬ��
�ᣬ��![]() ����MN�Ľ���ʽΪ
����MN�Ľ���ʽΪ![]() ֪
֪![]() ���ݴ˵�
���ݴ˵�![]() ���ٸ���
���ٸ���![]() �����κ��������ʽ�һ�����ɵã�
�����κ��������ʽ�һ�����ɵã�
��3������![]() �������������ľ��빫ʽ�õ�
�������������ľ��빫ʽ�õ�![]() �������ۣ�����ACD����ACΪֱ�DZߡ�CDΪб�ߺ���ACΪֱ�DZߡ�ADΪб�ߵ�ֱ��������ʱ���ֱ�ⷽ�����y���ɵõ���Ӧ��D�����ꣻ
�������ۣ�����ACD����ACΪֱ�DZߡ�CDΪб�ߺ���ACΪֱ�DZߡ�ADΪб�ߵ�ֱ��������ʱ���ֱ�ⷽ�����y���ɵõ���Ӧ��D�����ꣻ
�����ڵ���ACD����ACΪб�ߵ�ֱ��������ʱ��![]() ���ⷽ�̵õ�y��ֵ��Ȼ����ͼ�ο�ȷ����ACD�����������ʱ����D�������ȡֵ��Χ��
���ⷽ�̵õ�y��ֵ��Ȼ����ͼ�ο�ȷ����ACD�����������ʱ����D�������ȡֵ��Χ��
��1���������߹�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]()
���B����Ϊ![]()
���������߽���ʽΪ![]()
����![]() �����
�����![]()
���![]()
�������ߵĽ���ʽΪ![]()
�������ߵĽ���ʽΪ![]() ��
��
��2����P������Ϊ![]()
![]()
��ֱ��AC����ʽΪ![]()
����P��![]() �ᣬ��AC��H����PG��y����G
�ᣬ��AC��H����PG��y����G
![]()
��MN�Ľ���ʽΪ![]()
![]()
![]()
![]()
![]()
![]()
![]()
�ɶ��κ��������ʿ�֪����![]() ʱ��
ʱ��![]() ȡ�����ֵ�����ֵΪ
ȡ�����ֵ�����ֵΪ![]()
��![]() �����ֵΪ
�����ֵΪ![]() ��
��
��3������![]()
![]()
��![]()
����ACD����ACΪֱ�DZߡ�CDΪб�ߵ�ֱ��������ʱ
![]() ����
����![]()
���![]() �����ʱ
�����ʱ![]()
����ACD����ACΪֱ�DZߡ�ADΪб�ߵ�ֱ��������ʱ
![]() ����
����![]()
���![]() �����ʱ��
�����ʱ��![]()
���ϣ���D������Ϊ![]() ��
��![]() ��
��
�ڵ���ACD����ACΪб�ߵ�ֱ��������ʱ
![]() ����
����![]()
������![]()
���![]() ��
��![]()
�ʵ���ACD�����������ʱ����D�������ȡֵ��Χ��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
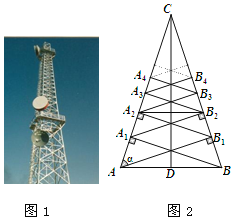
����Ŀ���ƶ�ͨ�Ź�˾����ĸּ��ź�������ͼ1��������һ�������ʾ��ͼ����ͼ2����CD�ǵ���������ABC�ױ��ϵĸߣ��ֱ����A����B�������Ĵ��߶Σ�����ֱ�ΪB1��A1���ٹ�A1��B1�ֱ��������Ĵ��߶����õĴ���ΪB2��A2����ͬ�����������εõ�����B3��A3��������ABΪ3�ף�sin����![]() ����ˮƽ����A2B2�ij���Ϊ��������
����ˮƽ����A2B2�ij���Ϊ��������
A. ![]() ��B. 2��C.
��B. 2��C. ![]() ��D.
��D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
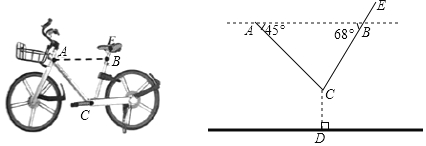
����Ŀ����ͼ��ʾ��һ����������ˮƽ�ĵ����ϣ�����ͷ�·�![]() ���������·�
���������·�![]() ����ƽ���ڵ����ͬһˮƽ���ϣ�
����ƽ���ڵ����ͬһˮƽ���ϣ�![]() ��
��![]() ֮��ľ���ԼΪ
֮��ľ���ԼΪ![]() ���ֲ��
���ֲ��![]() ��
��![]() ��
��![]() �ļнǷֱ�Ϊ
�ļнǷֱ�Ϊ![]() ��
��![]() ������
������![]() ������ľ���
������ľ���![]() Ϊ
Ϊ![]() ����������
����������![]() �����
�����![]() �ľ���
�ľ���![]() Ϊ
Ϊ![]() �����
�����![]() ������ľ��루�������һλС����.���ο����ݣ�
������ľ��루�������һλС����.���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c(a��0)�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� |
| ��4 |
| ��4 |
| 0 |
| �� |
(1)��������ߵı���ʽ��
(2)��֪��E(4�� y)�Ǹ��������ϵĵ㣬��E���������ߵĶԳ���ԳƵĵ�Ϊ��F�����E�͵�F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������н�����Ϊ����ȫ�н�ʦ���˶����������ֽ����еġ����˶�������������˱���![]() ����ʦij�ա����˶����еIJ����������ͳ�����������������µ�ͳ��ͼ����
����ʦij�ա����˶����еIJ����������ͳ�����������������µ�ͳ��ͼ����
���� | Ƶ�� | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
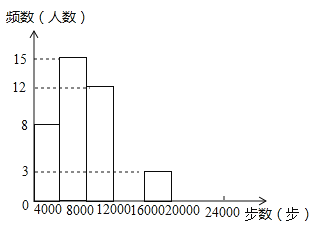
�����������Ϣ������������⣺
��1��д��![]() ��ֵ������ȫƵ���ֲ�ֱ��ͼ��
��ֵ������ȫƵ���ֲ�ֱ��ͼ��
��2������Լ��![]() ����ʦ����ϵ�������ݹ��������߲�������
����ʦ����ϵ�������ݹ��������߲�������![]() ��������
��������![]() �����Ľ�ʦ�ж�������
�����Ľ�ʦ�ж�������
��3�����ڱ�����Ľ�ʦ�У�ѡȡ�����߲�������![]() ��������
��������![]() ������������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ö���
������������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ö���![]() ��������
��������![]() �������ϵĸ��ʣ�
�������ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��ͼ1���ڡ�ABC�У���DE��BCʱ���Եõ�����ɱ����߶Σ��� ![]() ����
���� ![]() ����
���� ![]() ����֮������Ӧ�߶γ̱���ʱҲ�����Ƴ�DE��BC��
����֮������Ӧ�߶γ̱���ʱҲ�����Ƴ�DE��BC��
�������ã������ε��ڽ��ı�����ָ�����������θ����ϵ��ı��Σ�
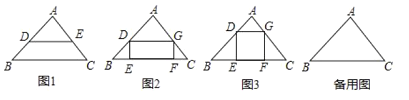
��1����ͼ2����֪����DEFG�ǡ�ABC��һ���ڽӾ��Σ�������DEFG��CB��������ƽ�Ƶþ���PBQH�����ж���D��E��F��G�Ķ�Ӧ��ֱ�ΪP��B��Q��H����ͼ2�л���ƽ�ƺ��ͼ�Σ�
��2���ڣ�1�����õ�ͼ���У�����CH���ӳ���BP���ӳ����ڵ�R������AR����֤��AR��BC��
��3����ͼ3��ijС����һ�������οյأ���֪��ABC�յصı�AB=400�ף�BC=600�ף���ABC=45�������ڡ�ABC�ڽ�һ���ڽӾ��ι㳡DEFG����E��F�ڱ�BC�ϣ���D��G�ֱ��ڱ�AB��AC�ϣ������������ಿ�ֽ���ֲ���̻�����Ҫ����ʹ����DEFG�ĶԽ���EG��̣����ڱ���ͼ�л���ʹ�Խ���EG��̵ľ��Σ�������Խ���EG����̾��루��Ҫ��֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����AOB��ͼ����1��������OA��ȡһ��C���Ե�OΪԲ�ģ�OC��Ϊ�뾶��![]() ��������OB�ڵ�D������CD��
��������OB�ڵ�D������CD��
��2���ֱ��Ե�C��DΪԲ�ģ�CD��Ϊ�뾶��������![]() �ڵ�M��N��
�ڵ�M��N��
��3������OM��MN��
����������ͼ���̼�����ͼ�Σ����н����д�����ǣ� ��

A. ��COM=��CODB. ��OM=MN������AOB=20��
C. MN��CDD. MN=3CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪�߳�Ϊ4�������θְ���һ������ʴ������AF��2��BF��1��Ϊ�˺����������ְ壮���������EABCD�ڽ�ȡһ�����ο�MDNP��ʹ��P��AB�ϣ���Ҫ����������ְ����������ʣ�
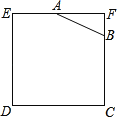
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֻ�ı�������![]() ����״���õ��ı���
����״���õ��ı���![]() ����
����![]() �����ı���
�����ı���![]() ��������
��������![]() ������ı��ǣ� ����
������ı��ǣ� ����
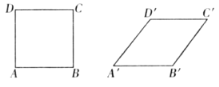
A.1:1B.2:3C.![]() :2D.3:4
:2D.3:4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com