
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
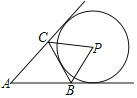
A.8B.10C.13D.14
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
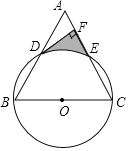
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余两人中随机选取一人打第一场,选中小莹的概率是________.
(2)如果确定小亮打第一场,用投掷硬币的方法确定小莹、小芳谁打第一场,并决定小亮做裁判,由小亮抛掷一枚硬币,规定正面朝上小莹胜,反面朝上小芳胜,最终胜两局以上者(包括两局)打第一场.小亮第一次投掷的结果是正面朝上,请用列表或画树状图的方法表示最后两次投掷硬币的所有情况,并求小芳打第一场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
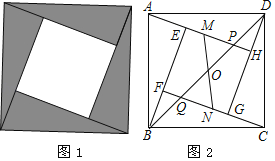
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作等边
的右侧作等边![]() .
.
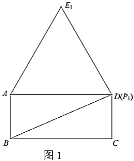
(1)①如图1,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,则点
,则点![]() 到
到![]() 的距离是________;
的距离是________;
②如图2,当点![]() 运动到点
运动到点![]() 落在
落在![]() 上时,记等边
上时,记等边![]() 为等边
为等边![]() .则等边
.则等边![]() 的边长
的边长![]() 是________;
是________;
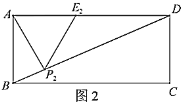
(2)如图3,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长;
的长;
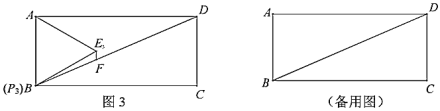
(3)①在上述变化过程中的点![]() ,
,![]() ,
,![]() 是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
②点![]() 的位置随着动点
的位置随着动点![]() 在线段
在线段![]() 上的位置变化而变化,猜想关于所有点
上的位置变化而变化,猜想关于所有点![]() 的位置的一个数学结论,试用一句话表述:______.
的位置的一个数学结论,试用一句话表述:______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com