
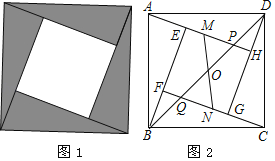
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇМведЫЌРћгУЯвЭМжЄУїСЫЙДЙЩЖЈРэЃЌетЪЧжјУћЕФедЫЌЯвЭМЃЈШчЭМ1ЃЉЃЎЫќЪЧгЩЫФИіШЋЕШЕФжБНЧШ§НЧаЮЦДГЩСЫФкЁЂЭтЖМЪЧе§ЗНаЮЕФУРРіЭМАИЃЎдкЯвЭМжаЃЈШчЭМ2ЃЉЃЌвбжЊЕуOЮЊе§ЗНаЮABCDЕФЖдНЧЯпBDЕФжаЕуЃЌЖдНЧЯпBDЗжБ№НЛAHЃЌCFгкЕуPЁЂQЃЎдке§ЗНаЮEFGHЕФEHЁЂFGСНБпЩЯЗжБ№ШЁЕуMЃЌNЃЌЧвMNОЙ§ЕуOЃЌШєMHЃН3MEЃЌBDЃН2MNЃН4![]() ЃЎдђЁїAPDЕФУцЛ§ЮЊ_____ЃЎ
ЃЎдђЁїAPDЕФУцЛ§ЮЊ_____ЃЎ
ЁОД№АИЁП5
ЁОНтЮіЁП
СЌНгFHЃЌзїEKЁЮMNЃЌOLЁЭDGЃЌЭЈЙ§е§ЗНаЮЕФаджЪКЭШЋЕШШ§НЧаЮЕФаджЪвдМАЙДЙЩЖЈРэПЩЧѓEMЃН1ЃЌПЩЕУEHЃН4ЃЌгЩЙДЙЩЖЈРэПЩЧѓHDЃН2ЃЌAHЃН6ЃЌгЩЦНааЯпЕФаджЪПЩЕУPHЃН1ЃЌМДПЩЧѓНтЃЎ
ШчЭМЃЌСЌНгFHЃЌзїEKЁЮMNЃЌOLЁЭDG
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌЧвBDЃН2MNЃН4![]()
ЁрMNЃН2![]() ЃЌABЃН2
ЃЌABЃН2![]()
ЁпЫФБпаЮEFGHЪЧе§ЗНаЮ
ЁрFOЃНHOЃЌEHЁЮFG
ЁрЁЯHMOЃНЁЯFNOЃЌЁЯMHOЃНЁЯNFOЃЌЧвFOЃНHO
ЁрЁїMHOЁеЁїFNOЃЈAASЃЉ
ЁрMHЃНFN
ЁпMHЃН3MEЃЌ
ЁрMHЃНFNЃН3EMЃЌEHЃНEFЃН4EM
ЁрEKЁЮKNЃЌEHЁЮFG
ЁрЫФБпаЮEMNKЪЧЦНааЫФБпаЮ
ЁрMNЃНEKЃН2![]() ЃЌKNЃНEM
ЃЌKNЃНEM
ЁрFKЃН2EM
ЁпEF2+FK2ЃНEK2ЃЌ
Ёр16EM2+4EM2ЃН20
ЁрEMЃН1
ЁрEHЃН4ЃЌ
ЁпAD2ЃНЃЈAE+4ЃЉ2+DH2ЃЌЧвAEЃНDH
ЁрDHЃНAEЃН2
ЁрAHЃН6
ЁпPHЁЮOL
Ёр![]()
ЁрPHЃН1
ЁрAPЃН5
ЁрSЁїAPDЃН![]() ЁС5ЁС2ЃН5
ЁС5ЁС2ЃН5
ЙЪД№АИЮЊЃК5.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() гы
гы![]() ЕФНЛЕуЃЌ
ЕФНЛЕуЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯЕФЖЏЕуЃЈЕу
БпЩЯЕФЖЏЕуЃЈЕу![]() ВЛгы
ВЛгы![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() ДЙжБ
ДЙжБ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎЯТСаЫФИіНсТлЃКЂй
ЃЎЯТСаЫФИіНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂмШє
ЃЛЂмШє![]() ЃЌдђ
ЃЌдђ![]() ЕФзюаЁжЕЪЧ1ЃЎЦфжае§ШЗНсТлЪЧЃЈ ЃЉ
ЕФзюаЁжЕЪЧ1ЃЎЦфжае§ШЗНсТлЪЧЃЈ ЃЉ
A.ЂйЂкЂлB.ЂйЂлЂмC.ЂйЂкЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮABCDжаЃЌЖдНЧЯпBDЫљдкЕФжБЯпЩЯгаСНЕуEЁЂFТњзуBE=DFЃЌСЌНгAEЁЂAFЁЂCEЁЂCFЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїADFЃЛ
ЃЈ2ЃЉЪдХаЖЯЫФБпаЮAECFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
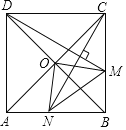
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌBCЃН4ЃЌЁбPгыЁїABCЕФБпЛђБпЕФбгГЄЯпЯрЧаЃЎШєЁбPАыОЖЮЊ2ЃЌЁїABCЕФУцЛ§ЮЊ5ЃЌдђЁїABCЕФжмГЄЮЊ( )
A.8B.10C.13D.14
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуAЁЂCЗжБ№дкxЁЂyжсЕФе§АыжсЩЯЃЌЖЅЕуBЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЕуMЪЧБпBCЩЯЕФвЛИіЖЏЕуЃЈВЛгыBЁЂCжиКЯЃЉЃЌЗДБШР§КЏЪ§![]() ЃЈkЃО0ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§ЕуMЧвгыБпABНЛгкЕуNЃЌСЌНгMNЃЎ
ЃЈkЃО0ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§ЕуMЧвгыБпABНЛгкЕуNЃЌСЌНгMNЃЎ
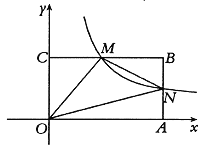
ЃЈ1ЃЉЕБЕуMЪЧБпBCЕФжаЕуЪБЃЌЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌЪджЄУїЃК![]() ЪЧвЛИіЖЈжЕЃЎ
ЪЧвЛИіЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
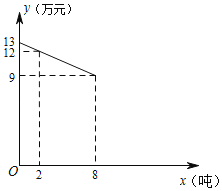
ЁОЬтФПЁПЮТжнВшЩНбюУЗУћбяжаЙњЃЌФГЙЋЫООгЊВшЩНбюУЗвЕЮёЃЌвд3ЭђдЊ/ЖжЕФМлИёТђШыбюУЗЃЌАќзАКѓжБНгЯњЪлЃЌАќзАГЩБОЮЊ1ЭђдЊ/ЖжЃЌЫќЕФЦНОљЯњЪлМлИёyЃЈЕЅЮЛЃКЭђдЊ/ЖжЃЉгыЯњЪлЪ§СПxЃЈ2ЁмxЁм10ЃЌЕЅЮЛЃКЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈ1ЃЉШєбюУЗЕФЯњЪлСПЮЊ6ЖжЪБЃЌЫќЕФЦНОљЯњЪлМлИёЪЧУПЖжЖрЩйЭђдЊЃП
ЃЈ2ЃЉЕБЯњЪлЪ§СПЮЊЖрЩйЪБЃЌИУОгЊетХњбюУЗЫљЛёЕУЕФУЋРћШѓЃЈwЃЉзюДѓЃПзюДѓУЋРћШѓЮЊЖрЩйЭђдЊЃПЃЈУЋРћШѓЃНЯњЪлзмЪеШыЉНјМлзмГЩБОЉАќзАзмЗбгУЃЉ
ЃЈ3ЃЉОЙ§ЪаГЁЕїВщЗЂЯжЃЌбюУЗЩюМгЙЄКѓВЛАќзАжБНгЯњЪлЃЌЦНОљЯњЪлМлИёЮЊ12ЭђдЊ/ЖжЃЎЩюМгЙЄЗбгУyЃЈЕЅЮЛЃКЭђдЊЃЉгыМгЙЄЪ§СПxЃЈЕЅЮЛЃКЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕЪЧyЃН![]() x+3ЃЈ2ЁмxЁм10ЃЉЃЎ
x+3ЃЈ2ЁмxЁм10ЃЉЃЎ
ЂйЕБИУЙЋЫОТђШыбюУЗЖрЩйЖжЪБЃЌВЩгУЩюМгЙЄЗНЪНгыжБНгАќзАЯњЪлЛёЕУУЋРћШѓвЛбљЃП
ЂкИУЙЋЫОТђШыбюУЗЖжЪ§дкЁЁ ЁЁЗЖЮЇЪБЃЌВЩгУЩюМгЙЄЗНЪНБШжБНгАќзАЯњЪлЛёЕУУЋРћШѓДѓаЉЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧвЛжжжННэКаЃЌгЩКаЩэКЭдВЛЁИЧзщГЩЃЌЭЈЙ§дВЛЁИЧЕФа§зЊРДПЊЙижННэКаЃЎШчЭМ2ЪЧЦфВрУцМђЛЏЪОвтЭМЃЌвбжЊОиаЮ![]() ЕФГЄ
ЕФГЄ![]() ЃЌПэ
ЃЌПэ![]() ЃЌдВЛЁИЧАхВрУц
ЃЌдВЛЁИЧАхВрУц![]() ЫљдкдВЕФдВаФ
ЫљдкдВЕФдВаФ![]() ЪЧОиаЮ
ЪЧОиаЮ![]() ЕФжааФЃЌШЦЕу
ЕФжааФЃЌШЦЕу![]() а§зЊПЊЙиЃЈЫљгаНсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉЃЎ
а§зЊПЊЙиЃЈЫљгаНсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉЃЎ
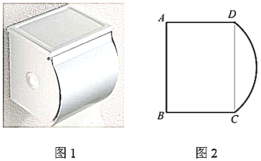 ЁЁЁЁЁЁ
ЁЁЁЁЁЁ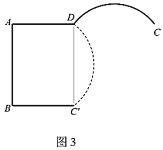
ЃЈ1ЃЉЧѓ![]() Ыљдк
Ыљдк![]() ЕФАыОЖГЄМА
ЕФАыОЖГЄМА![]() ЫљЖдЕФдВаФНЧЖШЪ§ЃЛ
ЫљЖдЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌЕБдВЛЁИЧАхВрУц![]() ДгЦ№ЪМЮЛжУ
ДгЦ№ЪМЮЛжУ![]() ШЦЕу
ШЦЕу![]() а§зЊ
а§зЊ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() дкетИіа§зЊЙ§ГЬжаЩЈЙ§ЕФЕФУцЛ§ЃЎ
дкетИіа§зЊЙ§ГЬжаЩЈЙ§ЕФЕФУцЛ§ЃЎ
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ШЁ3.14ЃЎ
ШЁ3.14ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
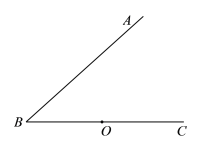
ЁОЬтФПЁПШчЭМЃЌЕуOЮЊЁЯABCЕФБп![]() ЩЯЕФвЛЕуЃЌЙ§ЕуOзїOMЁЭABгкЕу
ЩЯЕФвЛЕуЃЌЙ§ЕуOзїOMЁЭABгкЕу![]() ЃЌЕНЕу
ЃЌЕНЕу![]() ЕФОрРыЕШгкЯпЖЮOMЕФГЄЕФЫљгаЕузщГЩЭМаЮ
ЕФОрРыЕШгкЯпЖЮOMЕФГЄЕФЫљгаЕузщГЩЭМаЮ![]() ЃЎЭМаЮWгыЩфЯп
ЃЎЭМаЮWгыЩфЯп![]() НЛгкEЃЌFСНЕу(ЕудкЕуFЕФзѓВр).
НЛгкEЃЌFСНЕу(ЕудкЕуFЕФзѓВр).
ЃЈ1ЃЉЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌШчЙћBE=2ЃЌ
ЃЌШчЙћBE=2ЃЌ![]() ЃЌЧѓMHЕФГЄЃЛ
ЃЌЧѓMHЕФГЄЃЛ
ЃЈ2ЃЉНЋЩфЯпBCШЦЕуBЫГЪБеыа§зЊЕУЕНЩфЯпBDЃЌЪЙЕУЁЯ![]()
![]() ЃЌХаЖЯЩфЯпBDгыЭМаЮ
ЃЌХаЖЯЩфЯпBDгыЭМаЮ![]() ЙЋЙВЕуЕФИіЪ§ЃЌВЂжЄУїЃЎ
ЙЋЙВЕуЕФИіЪ§ЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
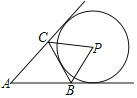
ЁОЬтФПЁПШчЭМЃЌдкЁбOжаЃЌЯвABДЙжБЦНЗжАыОЖOCЃЌДЙзуЮЊDЃЎШєЕуPЪЧЁбOЩЯвьгкЕуAЃЌBЕФШЮвтвЛЕуЃЌдђЁЯAPB=ЃЈ ЃЉ
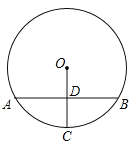
A.30ЁуЛђ60ЁуB.60ЁуЛђ150ЁуC.30ЁуЛђ150ЁуD.60ЁуЛђ120Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com