【题目】如图，在⊙O中，弦AB垂直平分半径OC，垂足为D．若点P是⊙O上异于点A，B的任意一点，则∠APB=（ ）
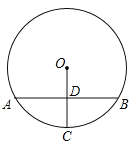
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
【答案】D
【解析】
利用垂径定理及已知可得到∠OAD=30°，再求出∠AOB的度数，再分情况讨论：当点P在优弧AB上时，利用圆周角定理就可取出∠P的度数；当点P在劣弧上时，利用圆内接四边形的对角互补，就可求出∠AP1B的度数．
连接OA，OB，
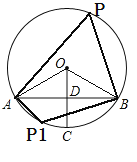
∵ 弦AB垂直平分半径OC
∴OD=
OA，
∴∠OAD=30°，
∵OA=OB
∴∠OAB=∠OBA=30°，
∴∠AOB=180°-∠OAB-∠OBA=180°-30°-30°=120°；
当点P在优弧AB上时
∠APB=∠AOB=×120°=60°；
当点P在劣弧上时，
∠APB+∠AP1B=180°
∴∠AP1B=180°-60°=120°．
∴∠APB=120°或60°．
故答案为：D．
天天练口算系列答案科目：初中数学 来源： 题型：
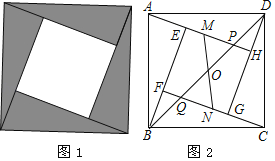
【题目】我国古代数学家赵爽利用弦图证明了勾股定理，这是著名的赵爽弦图（如图1）．它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案．在弦图中（如图2），已知点O为正方形ABCD的对角线BD的中点，对角线BD分别交AH，CF于点P、Q．在正方形EFGH的EH、FG两边上分别取点M，N，且MN经过点O，若MH＝3ME，BD＝2MN＝4
．则△APD的面积为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形
中，
，
，点
，
分别在边
，
上，
，连接
，
．动点
在
上从点向终点匀速运动，同时，动点
在射线
．上从点
沿方向匀速运动，当点运动到EF的中点时，点恰好与点
重合，点到达终点时，， 同时停止运动．
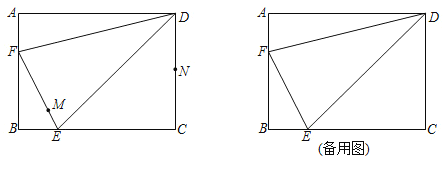
（1）求的长．
（2）设
，
，求
关于
的函数表达式，并写出自变的取值范围．
（3）连接
，当与
的一边平行时，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
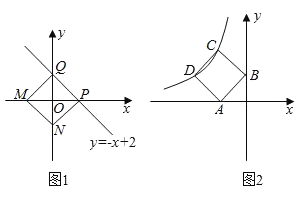
【题目】已知：点M、N分别是x轴y轴上的动点，点P、Q是某个函数图象上的点，当四边形MNPQ为正方形时，称这个正方形为此函数的“梦幻正方形”例如：如图1所示，正方形MNPQ是一次函数y＝﹣x+2的其中一个“梦幻正方形”．
（1）若某函数是y＝x+5，求它的图象的所有“梦幻正方形”的边长；
（2）若某函数是反比例函数y＝
（k＜0）（如图2所示），它的图象的“梦幻正方形”ABCD，D（﹣4，m）（m＜4）在反比例函数图象上，求m的值及反比例函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
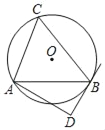
【题目】如图，⊙O的半径为5，△ABC是⊙O的内接三角形，AB＝8．AD和过点B的切线互相垂直，垂足为D．
（1）求证：∠BAD+∠C＝90°；
（2）求线段AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，
的三个顶点坐标分别为
、
、
．
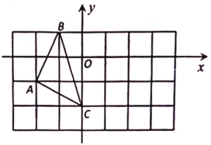
（1）点
关于坐标原点
对称的点的坐标为______；
（2）将绕着点
顺时针旋转
，画出旋转后得到的
；
（3）在（2）中，求边
所扫过区域的面积是多少？（结果保留
）．
（4）若
、、三点的横坐标都加3，纵坐标不变，图形的位置发生怎样的变化？
查看答案和解析>>
科目：初中数学 来源： 题型：
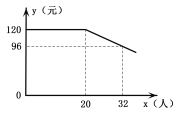
【题目】随着人们生活水平的提高，短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目，团队人均报名费用y（元）与团队报名人数x（人）之间的函数关系如图所示，旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w（元）.
（1）直接写出当x≥20时，y与x之间的函数关系式及自变量x的取值范围；
（2）儿童节当天旅行社收到某个团队的总报名费为3000元，报名旅游的人数是多少？
（3）当一个团队有多少人报名时，旅行社收到的总报名费最多？最多总报名费是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一段抛物线
向右依次平移3个单位，得到第2，3，4段抛物线，设这四段抛物线分别为
，若直线
与第四段抛物线
有唯一公共点，则
的取值范围是（ ）
A.
B.
C.或D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
