练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

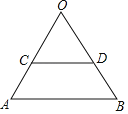
    【题目】如图，△ABO是正三角形，CD∥AB，把△ABO绕△OCD的内心P旋转180°得到△EFG

    （1）在图中画出点P和△EFG，保留画图痕迹，简要说明理由

    （2）若AO＝3，CD＝2，求A点运动到E点路径的长．

    【答案】（1）详见解析；（2）π．

    【解析】

    （1）根据正三角形的三线合一的性质，先画出△OCD的角平分线的交点，即为点P，再把△ABO绕着△OCD的内心P旋转180°得到△EFG即可；

    （2）先根据等边三角形的性质求出OH和△OCD的高，进而求得额OP、PH的长，再根据勾股定理求得PA的长，由于点A运动到点D的运动路线是半圆，进而由弧长公式或圆的周长来求得答案即可．

    解：（1）点P和△EFG如图所示．

    （2）延长OP交CD于G，交AB于H，

    ∵OA＝3，CD＝2，

    ∴OP＝2，OH＝，

    ∴PH＝OH﹣OP＝，AH＝HB＝，

    ∴

    ∴A点运动到E点路径的长＝．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在中，，，以为边在的另一侧作，点为射线上任意一点，在射线上截取，连接、、．

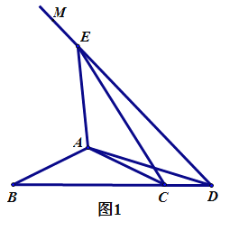
    （1）如图1，当点落在线段的延长线上时，的度数为__________．

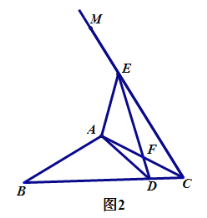
    （2）如图2，当点落在线段（不含边界）上时，与交于点，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；

    （3）在（2）的条件下，若，求的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

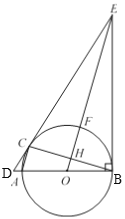
    【题目】如图，AB是⊙O的直径，C 是⊙O上一点，过点C 作⊙O的切线，交BA的延长线交于点D，过点B 作BE⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC．

    （1）求证：∠ECB=∠EBC；

    （2）连接BF，CF，若BF=5，sin∠FBC=，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l和双曲线y=(k>0)交于A、B两点，P是线段AB上的点(不与A、B重合)，过点A、B、P分别向x轴作垂线，垂足分别为C、D、E，连接OA、OB、OP，设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3，则( )

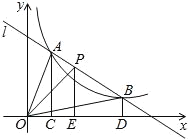
    A.S1＜S2＜S3B.S1＞S2＞S3C.S1＝S2＞S3D.S1＝S2＜S3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现

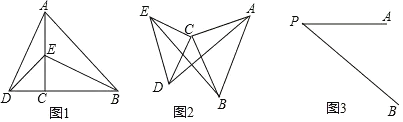
    如图1，△ACB和△DCE均为等腰直角三角形，∠ACB=90°，B，C，D在一条直线上，填空：线段AD，BE之间的关系为

    （2）拓展探究

    如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，请判断AD，BE的关系，并说明理由．

    （3）解决问题

    如图3，线段PA=，点B是线段PA外一点，PB=3，连接AB绕点A逆时针旋转90°得到线段AC，随着点B的位置变化，直接写出PC的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

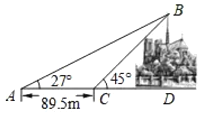
    【题目】当地时间2019年4月15日下午，法国巴黎圣母院发生火灾，大火烧毁了巴黎圣母院后塔的塔顶．烧毁前，为测量此塔顶的高度，在地面选取了与塔底共线的两点、，、在的同侧，在处测量塔顶的仰角为27°，在处测量塔顶的仰角为45°，到的距离是89.5米．设的长为米，则下列关系式正确的是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

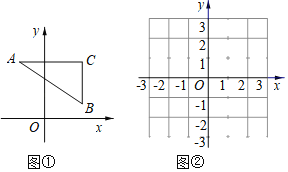
    【题目】如图①，在平面直角坐标系中，当线段AB与坐标轴不垂直时，以线段AB为斜边作Rt△ABC，且边BC⊥x轴，则称AC+BC的值为线段AB的直角距离，记作L（AB）；当线段AB与坐标轴垂直时，线段AB的直角距离不存在．

    （1）在平面直角坐标系中，A（1，4），B（4，2），求L（AB）．

    （2）在平面直角坐标系中，点A与坐标原点重合，点B（x，y），且L（AB）＝2．

    ①当点B（x，y）在第一象限时，易知AC＝x，BC＝y．由AC+BC＝L（AB），可得y与x之间的函数关系式为　 　，其中x的取值范围是　 　，在图②中画出这个函数的图象．

    ②请模仿①的思考过程，分别探究点B在其它象限的情形，仍然在图②中分别画出点B在二、三、四象限时，y与x的函数图象．（不要求写出探究过程）

    （3）在平面直角坐标系中，点A（1，1），在抛物线y＝a（x﹣h）2+5上存在点B，使得2≤L（AB）≤4．

    ①当a＝﹣时，直接写出h的取值范围．

    ②当h＝0，且△ABC是等腰直角三角形时，直接写出a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

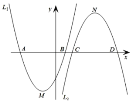
    【题目】如图，已知二次函数：和二次函数：图象的顶点分别为、，与轴分别相交于、两点（点在点的左边）和、两点（点在点的左边），

    　　　　　

    （1）函数的顶点坐标为______；当二次函数，的值同时随着的增大而增大时，则的取值范围是_______；

    （2）判断四边形的形状（直接写出，不必证明）；

    （3）抛物线，均会分别经过某些定点；

    ①求所有定点的坐标；

    ②若抛物线位置固定不变，通过平移抛物线的位置使这些定点组成的图形为菱形，则抛物线应平移的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

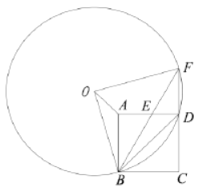
    【题目】如图，在正方形中，点在边上运动（不运动至两端点），射线，交于点，为的外接圆，连结，，．

    （1）求的度数．

    （2）求证：．

    （3）若正方形的边长为．

    ①当为中点时，求四边形的面积．

    ②设，交于点，设，，的面积分别为，，，当平分时，_________（直接写出答案）．

    查看答案和解析>>

    同步练习册答案