
°æƒø°ø∂‘”⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–µƒµ„P∫Õ°—C£¨∏¯≥ˆ»Áœ¬µƒ∂®“£∫»Ù°—C…œ¥Ê‘⁄¡Ω∏ˆµ„A°¢B£¨ πµ√°œAPB£Ω60°„£¨‘Ú≥∆PŒ™°—Cµƒø… ”µ„£Æ
£®1£©µ±°—Oµƒ∞Îæ∂Œ™1 ±£¨
¢Ÿ‘⁄µ„![]() °¢E(1£¨1)°¢F(3£¨0)÷–£¨°—Oµƒø… ”µ„ «______£Æ
°¢E(1£¨1)°¢F(3£¨0)÷–£¨°—Oµƒø… ”µ„ «______£Æ
¢⁄π˝µ„M(4£¨0)◊˜÷±œfll£∫y=kx+b£¨»Ù÷±œfll…œ¥Ê‘⁄°—Oµƒø… ”µ„£¨«Ûbµƒ»°÷µ∑∂Œß£ª
£®2£©»ÙT(t£¨0)£¨°—Tµƒ∞Îæ∂Œ™1£¨÷±œfly=![]() …œ¥Ê‘⁄°—Tµƒø… ”µ„£¨«“À˘”–ø… ”µ„ππ≥…µƒœfl∂Œ≥§∂»Œ™n£¨»Ù
…œ¥Ê‘⁄°—Tµƒø… ”µ„£¨«“À˘”–ø… ”µ„ππ≥…µƒœfl∂Œ≥§∂»Œ™n£¨»Ù![]() £¨÷±Ω”–¥≥ˆt µƒ»°÷µ∑∂Œß£Æ
£¨÷±Ω”–¥≥ˆt µƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©¢ŸD°¢E£¨¢⁄![]() £ª£®2£©
£ª£®2£©![]() ªÚ
ªÚ![]()
°æΩ‚Œˆ°ø
£®1£©¢Ÿ∏˘æ›Ã‚“‚柿˝Àµ√˜º¥ø…£ª
¢⁄µ±÷±œfll”Î∞Îæ∂Œ™2µƒ°—Oœ‡«– ±£¨¿˚”√sin°œAMO£Ω![]() £¨ø…«Ûµ√°œAMO£Ω30°„£¨Ω¯∂¯ø…«Ûµ√OE≥§£¨¥”∂¯ø…µ√bµƒ»°÷µ∑∂Œß£ª
£¨ø…«Ûµ√°œAMO£Ω30°„£¨Ω¯∂¯ø…«Ûµ√OE≥§£¨¥”∂¯ø…µ√bµƒ»°÷µ∑∂Œß£ª
£®2£©µ±t£æ0 ±£¨œ»«Û÷±œfly£Ω![]() ”Î∞Îæ∂Œ™2µƒ°—Tœ‡«– ±µƒtµƒ÷µ£¨‘Ÿ«Û÷±œfly£Ω
”Î∞Îæ∂Œ™2µƒ°—Tœ‡«– ±µƒtµƒ÷µ£¨‘Ÿ«Û÷±œfly£Ω![]() ”Î∞Îæ∂Œ™2µƒ°—Tœ‡Ωª«“À˘Ωÿœfl∂Œ≥§Œ™
”Î∞Îæ∂Œ™2µƒ°—Tœ‡Ωª«“À˘Ωÿœfl∂Œ≥§Œ™![]() ±µƒtµƒ÷µ£¨Ω¯∂¯«Ûµ√tµƒ»°÷µ∑∂Œß£Æ
±µƒtµƒ÷µ£¨Ω¯∂¯«Ûµ√tµƒ»°÷µ∑∂Œß£Æ
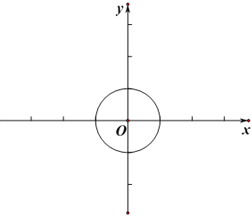
Ω‚£∫£®1£©¢Ÿ»ÁÕº£¨π˝µ„D◊˜DA°Œx÷·£¨DB°Œy÷·£¨ø…µ√°œADB£Ω90°„£¨µ±µ„A°¢B‘⁄‘≤…œ‘Ω¿¥‘ΩøøΩ¸ ±£¨°œADBø…“‘Œ™60°„£¨‘Úµ„D «ø… ”µ„£ª
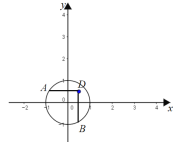
»ÁÕº£¨π˝µ„E◊˜°—Oµƒ«–œflEA°¢EB£¨‘Ú°œOAE£Ω°œOBE £Ω90°„
”÷°fl°œAOB£Ω90°„£¨°‡°œE£Ω90°„£¨
µ±µ„A°¢B‘⁄‘≤…œ‘Ω¿¥‘ΩøøΩ¸ ±£¨°œAEBø…“‘Œ™60°„£¨‘Úµ„E «ø… ”µ„£ª
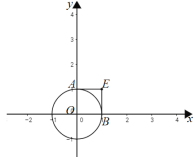
”…“‚ø…÷™£¨µ±µ„P‘⁄°—OÕ‚ ±£¨π˝µ„P◊˜°—Oµƒ«–œflPA°¢PB£¨‘Ú¥À ±°œAPB◊Ó¥Û£¨»Ù°œAPB°›60°„£¨‘Ú°—O…œ“ª∂®¥Ê‘⁄¡Ω∏ˆµ„A°¢B£¨ πµ√°œAPB£Ω60°„£Æ
»ÁÕº£¨π˝µ„P◊˜°—Oµƒ«–œflPA°¢PB£¨µ±°œAPB£Ω60°„ ±£¨‘Ú°œAPO£Ω°œBPO£Ω30°„£¨
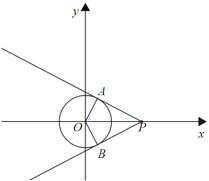
‘⁄Rt°˜AOP÷–£¨sin°œAPO£Ω![]() £¨
£¨
°flOA£Ω1£¨
°‡OP£Ω2
°‡µ±OP°‹2 ±£¨°—O“ª∂®”–ø… ”µ„£¨µ±OP£æ2 ±£¨°—O√ª”–ø… ”µ„£Æ
°flµ„F£®3,0£©£¨
°‡OF£Ω3£æ2£¨
°‡µ„F≤ª «ø… ”µ„
π ¥∞∏Œ™£∫D°¢E£Æ
¢⁄”…¢Ÿµ√£¨»Ù÷±œfll…œ¥Ê‘⁄°—Oµƒø… ”µ„£¨‘Ú÷±œfll”Î∞Îæ∂Œ™2µƒ°—Oœ‡«–ªÚœ‡Ωª£ª
»ÁÕº£¨µ±÷±œfll”Î∞Îæ∂Œ™2µƒ°—Oœ‡«– ±£¨
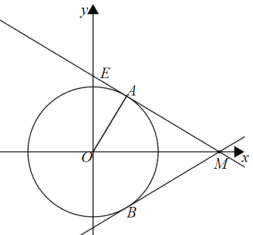
°flM(4£¨0)£¨
°‡OM£Ω4£¨
°‡‘⁄Rt°˜AOM÷–£¨sin°œAMO£Ω![]() £¨
£¨
°‡°œAMO£Ω30°„£¨
°‡‘⁄Rt°˜EOM÷–£¨tan°œEMO£Ω![]() £¨
£¨
°‡![]() £¨
£¨
°‡»Ù÷±œfll…œ¥Ê‘⁄°—Oµƒø… ”µ„£¨«Ûbµƒ»°÷µ∑∂ŒßŒ™![]() £ª
£ª
£®2£©µ±y£Ω0 ±£¨![]() £Ω0£¨
£Ω0£¨
Ω‚µ√£¨x£Ω![]() £¨‘Ú÷±œfll”Îx÷·µƒΩªµ„◊¯±ÍŒ™£®
£¨‘Ú÷±œfll”Îx÷·µƒΩªµ„◊¯±ÍŒ™£®![]() £¨0£©£¨
£¨0£©£¨
µ±x£Ω0 ±£¨y£Ω![]() £¨‘Ú÷±œfll”Îy÷·µƒΩªµ„◊¯±ÍŒ™£®0£¨
£¨‘Ú÷±œfll”Îy÷·µƒΩªµ„◊¯±ÍŒ™£®0£¨![]() £©£¨
£©£¨
°fl÷±œfly£Ω![]() …œ¥Ê‘⁄°—Tµƒø… ”µ„£¨«“°—Tµƒ∞Îæ∂Œ™1£¨
…œ¥Ê‘⁄°—Tµƒø… ”µ„£¨«“°—Tµƒ∞Îæ∂Œ™1£¨
°‡÷±œfly£Ω![]() ”Î∞Îæ∂Œ™2µƒ°—Tœ‡ΩªªÚœ‡«–
”Î∞Îæ∂Œ™2µƒ°—Tœ‡ΩªªÚœ‡«–
µ±t£æ0 ±£¨
»ÁÕº£¨µ±÷±œfly£Ω![]() ”Î∞Îæ∂Œ™2µƒ°—Tœ‡«– ±£¨
”Î∞Îæ∂Œ™2µƒ°—Tœ‡«– ±£¨
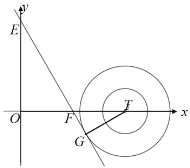
°flE£®0£¨![]() £©£¨F£®
£©£¨F£®![]() £¨0£©£¨
£¨0£©£¨
°‡OE£Ω![]() £¨OF£Ω
£¨OF£Ω![]() £¨
£¨
°‡‘⁄Rt°˜EOF÷–£¨tan°œEFO£Ω £¨
£¨
°‡°œTFG£Ω°œEFO£Ω60°„£¨
°flT£®t£¨0£©£¨
°‡TF£Ω![]() £¨
£¨
°‡‘⁄Rt°˜TGF÷–£¨sin°œTFG£Ω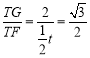 £¨
£¨
°‡![]() £¨
£¨
»ÁÕº£¨µ±÷±œfly£Ω![]() ”Î∞Îæ∂Œ™2µƒ°—Tœ‡Ωª«“CD£Ω
”Î∞Îæ∂Œ™2µƒ°—Tœ‡Ωª«“CD£Ω![]() ±£¨
±£¨
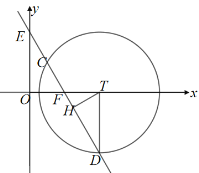
π˝µ„T◊˜TH°ÕCD£¨‘Ú![]()
‘⁄Rt°˜THD÷–£¨cos°œTDH£Ω![]() £¨
£¨
°‡°œTDH£Ω30°„£¨
”÷°fl°œTFD£Ω60°„£¨
°‡°œDTF£Ω90°„£¨
°‡‘⁄Rt°˜TFD÷–£¨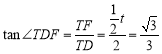 £¨
£¨
°‡![]() £¨
£¨
°fl![]() £¨
£¨
°‡![]() £¨
£¨
Õ¨¿Ì£¨µ±t£º0 ±£¨![]()
◊€…œÀ˘ ˆ£¨tµƒ»°÷µ∑∂ŒßŒ™£∫![]() ªÚ
ªÚ![]()


 ˝—ß∞¬»¸ ÓºŸÃÏÃÏ¡∑ƒœæ©¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
˝—ß∞¬»¸ ÓºŸÃÏÃÏ¡∑ƒœæ©¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏ ƒœ¥ÛΩÃ∏®«¿œ»∆≈‹ ÓºŸœŒΩ”ΩÃ≥Ü橥ۗß≥ˆ∞Ê…Áœµ¡–¥∞∏
ƒœ¥ÛΩÃ∏®«¿œ»∆≈‹ ÓºŸœŒΩ”ΩÃ≥Ü橥ۗß≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∂•µ„Œ™£®![]() £¨
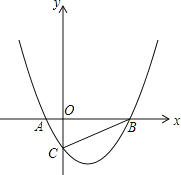
£¨![]() £©µƒ≈◊ŒÔœflΩªy÷·”⁄µ„C£®0£¨©Å2£©£¨Ωªx÷·”⁄µ„A£¨B£®µ„A‘⁄µ„Bµƒ◊Û≤‡£©£ÆPµ„ «y÷·…œ“ª∂ص„£¨Qµ„ «≈◊ŒÔœfl…œ“ª∂ص„£Æ
£©µƒ≈◊ŒÔœflΩªy÷·”⁄µ„C£®0£¨©Å2£©£¨Ωªx÷·”⁄µ„A£¨B£®µ„A‘⁄µ„Bµƒ◊Û≤‡£©£ÆPµ„ «y÷·…œ“ª∂ص„£¨Qµ„ «≈◊ŒÔœfl…œ“ª∂ص„£Æ
£®1£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©Pµ„‘À∂صΩ∫ŒŒª÷√ ±£¨°˜POA”ΰ˜ABCœ‡À∆£ø≤¢«Û≥ˆ¥À ±Pµ„µƒ◊¯±Í£ª
£®3£©µ±“‘A°¢B°¢P°¢QÀƒµ„Œ™∂•µ„µƒÀƒ±fl–ŒŒ™∆Ω––Àƒ±fl–Œ ±£¨«ÛQµ„µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
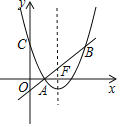
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨≈◊ŒÔœfly£Ωax2+bx+c”Î÷±œfll£∫y£Ωkx+m£®k£æ0£©Ωª”⁄A£®1£¨0£©£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄C£®0£¨3£©£¨∂‘≥∆÷·Œ™÷±œflx£Ω2£Æ
£®1£©«Î÷±Ω”–¥≥ˆ∏√≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©…Ë÷±œfll”Î≈◊ŒÔœflµƒ∂‘≥∆÷·µƒΩªµ„Œ™F£¨‘⁄∂‘≥∆÷·”“≤‡µƒ≈◊ŒÔœfl…œ”–“ªµ„G£¨»Ù![]() £¨«“S°˜BAG£Ω6£¨«Ûµ„Gµƒ◊¯±Í£ª
£¨«“S°˜BAG£Ω6£¨«Ûµ„Gµƒ◊¯±Í£ª
£®3£©»Ù‘⁄÷±œfl![]() …œ”–«“÷ª”–“ªµ„P£¨ π°œAPB£Ω90°„£¨«Ûkµƒ÷µ£Æ
…œ”–«“÷ª”–“ªµ„P£¨ π°œAPB£Ω90°„£¨«Ûkµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
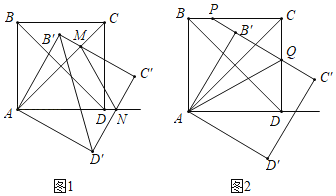
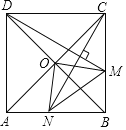
°æƒø°ø»ÁÕºΩ´’˝∑Ω–ŒABCD»∆µ„AÀ≥ ±’Ζ˝◊™Ω«∂»¶¡£®0°„£º¶¡£º90°„£©µ√µΩ’˝∑Ω–ŒAB°‰C°‰D°‰£Æ
£®1£©»ÁÕº1£¨B°‰C°‰”ÎACΩª”⁄µ„M£¨C°‰D°‰”ÎADÀ˘‘⁄÷±œflΩª”⁄µ„N£¨»ÙMN°ŒB°‰D°‰£¨«Û¶¡£ª
£®2£©»ÁÕº2£¨C°‰B°‰”ÎCDΩª”⁄µ„Q£¨—”≥§C°‰B°‰”ÎBCΩª”⁄µ„P£¨µ±¶¡£Ω30°„ ±£Æ
¢Ÿ«Û°œDAQµƒ∂» ˝£ª
¢⁄»ÙAB£Ω6£¨«ÛPQµƒ≥§∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
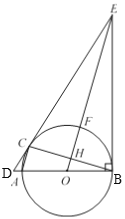
°æƒø°ø»ÁÕº£¨AB «°—Oµƒ÷±æ∂£¨C «°—O…œ“ªµ„£¨π˝µ„C ◊˜°—Oµƒ«–œfl£¨ΩªBAµƒ—”≥§œflΩª”⁄µ„D£¨π˝µ„B ◊˜BE°ÕBA£¨ΩªDC—”≥§œfl”⁄µ„E£¨¡¨Ω”OE£¨Ωª°—O”⁄µ„F£¨ΩªBC”⁄µ„H£¨¡¨Ω”AC£Æ
£®1£©«Û÷§£∫°œECB=°œEBC£ª
£®2£©¡¨Ω”BF£¨CF£¨»ÙBF=5£¨sin°œFBC=![]() £¨«ÛACµƒ≥§£Æ
£¨«ÛACµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
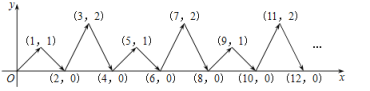
°æƒø°ø»ÁÕº£¨∂ص„![]() ‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–∞¥Õº÷–º˝Õ∑À˘ 浃∑ΩœÚ‘À∂Ø£¨µ⁄1¥Œ¥”‘≠µ„‘À∂صΩ(1£¨1)£¨µ⁄2¥ŒΩ”◊≈‘À∂ØµΩµ„(2£¨0)£¨µ⁄3¥ŒΩ”◊≈‘À∂ØµΩµ„(3£¨2)£¨£Æ£Æ£Æ∞¥’‚—˘µƒ‘À∂Øπʬ…£¨æ≠π˝2019¥Œ‘À∂Ø∫Û£¨∂ص„
‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–∞¥Õº÷–º˝Õ∑À˘ 浃∑ΩœÚ‘À∂Ø£¨µ⁄1¥Œ¥”‘≠µ„‘À∂صΩ(1£¨1)£¨µ⁄2¥ŒΩ”◊≈‘À∂ØµΩµ„(2£¨0)£¨µ⁄3¥ŒΩ”◊≈‘À∂ØµΩµ„(3£¨2)£¨£Æ£Æ£Æ∞¥’‚—˘µƒ‘À∂Øπʬ…£¨æ≠π˝2019¥Œ‘À∂Ø∫Û£¨∂ص„![]() µƒ◊¯±ÍŒ™___________£Æ
µƒ◊¯±ÍŒ™___________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨÷±œfll∫ÕÀ´«˙œfly=![]() (k>0)Ωª”⁄A°¢B¡Ωµ„£¨P «œfl∂ŒAB…œµƒµ„(≤ª”ÎA°¢B÷ÿ∫œ)£¨π˝µ„A°¢B°¢P∑÷±œÚx÷·◊˜¥πœfl£¨¥π◊„∑÷±Œ™C°¢D°¢E£¨¡¨Ω”OA°¢OB°¢OP£¨…Ë°˜AOCµƒ√ʪ˝Œ™S1°¢°˜BODµƒ√ʪ˝Œ™S2°¢°˜POEµƒ√ʪ˝Œ™S3£¨‘Ú( )
(k>0)Ωª”⁄A°¢B¡Ωµ„£¨P «œfl∂ŒAB…œµƒµ„(≤ª”ÎA°¢B÷ÿ∫œ)£¨π˝µ„A°¢B°¢P∑÷±œÚx÷·◊˜¥πœfl£¨¥π◊„∑÷±Œ™C°¢D°¢E£¨¡¨Ω”OA°¢OB°¢OP£¨…Ë°˜AOCµƒ√ʪ˝Œ™S1°¢°˜BODµƒ√ʪ˝Œ™S2°¢°˜POEµƒ√ʪ˝Œ™S3£¨‘Ú( )
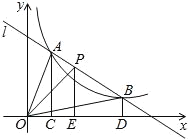
A.S1£ºS2£ºS3B.S1£æS2£æS3C.S1£ΩS2£æS3D.S1£ΩS2£ºS3
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
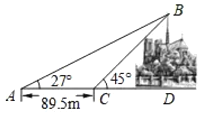
°æƒø°øµ±µÿ ±º‰2019ƒÍ4‘¬15»’œ¬ŒÁ£¨∑®π˙∞Õ¿Ë •ƒ∏‘∫∑¢…˙ª‘÷£¨¥Ûª…’ªŸ¡À∞Õ¿Ë •ƒ∏‘∫∫ÛÀ˛µƒÀ˛∂•£Æ…’ªŸ«∞£¨Œ™≤‚¡ø¥ÀÀ˛∂•![]() µƒ∏fl∂»£¨‘⁄µÿ√Ê—°»°¡À”ÎÀ˛µ◊
µƒ∏fl∂»£¨‘⁄µÿ√Ê—°»°¡À”ÎÀ˛µ◊![]() π≤œflµƒ¡Ωµ„
π≤œflµƒ¡Ωµ„![]() °¢
°¢![]() £¨
£¨![]() °¢
°¢![]() ‘⁄
‘⁄![]() µƒÕ¨≤‡£¨‘⁄
µƒÕ¨≤‡£¨‘⁄![]() ¥¶≤‚¡øÀ˛∂•
¥¶≤‚¡øÀ˛∂•![]() µƒ—ˆΩ«Œ™27°„£¨‘⁄
µƒ—ˆΩ«Œ™27°„£¨‘⁄![]() ¥¶≤‚¡øÀ˛∂•
¥¶≤‚¡øÀ˛∂•![]() µƒ—ˆΩ«Œ™45°„£¨
µƒ—ˆΩ«Œ™45°„£¨![]() µΩ
µΩ![]() µƒæ‡¿Î «89.5√◊£Æ…Ë
µƒæ‡¿Î «89.5√◊£Æ…Ë![]() µƒ≥§Œ™
µƒ≥§Œ™![]() √◊£¨‘Úœ¬¡–πÿœµ Ω’˝»∑µƒ «£® £©
√◊£¨‘Úœ¬¡–πÿœµ Ω’˝»∑µƒ «£® £©
A.![]() B.
B.![]()
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨
÷–£¨![]() «∂‘Ω«œfl
«∂‘Ω«œfl![]() ”Î
”Î![]() µƒΩªµ„£¨
µƒΩªµ„£¨![]() «
«![]() ±fl…œµƒ∂ص„£®µ„
±fl…œµƒ∂ص„£®µ„![]() ≤ª”Î
≤ª”Î![]() ÷ÿ∫œ£©£¨π˝µ„
÷ÿ∫œ£©£¨π˝µ„![]() ◊˜
◊˜![]() ¥π÷±
¥π÷±![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £Æœ¬¡–Àƒ∏ˆΩ·¬€£∫¢Ÿ
£Æœ¬¡–Àƒ∏ˆΩ·¬€£∫¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £ª¢‹»Ù
£ª¢‹»Ù![]() £¨‘Ú
£¨‘Ú![]() µƒ◊Ó–°÷µ «1£Æ∆‰÷–’˝»∑Ω·¬€ «£® £©
µƒ◊Ó–°÷µ «1£Æ∆‰÷–’˝»∑Ω·¬€ «£® £©
A.¢Ÿ¢⁄¢€B.¢Ÿ¢€¢‹C.¢Ÿ¢⁄¢‹D.¢⁄¢€¢‹
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com