
【题目】如图,在矩形纸片 ABCD 中,AD=5cm,AB=4cm,将矩形纸片 ABCD 沿直线l 折叠,使点 A 落在边 BC 上的 A'处,当直线 l 恰好过点 D 时,用直尺和圆规在图中作出直线 l,(保留作图 痕迹,不写作法),设点 A'与点 B 的距离为 x cm.并求出 x 的值.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
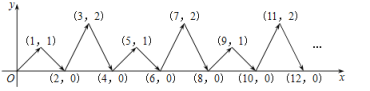
【题目】如图,动点![]() 在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),...按这样的运动规律,经过2019次运动后,动点
在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),...按这样的运动规律,经过2019次运动后,动点![]() 的坐标为___________.
的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个布袋,红布袋中有两个完全相同的小球,分别标有数字2和4.黄布袋中有三个完全相同的小球,分别标有数字﹣2,﹣4和﹣6.小贤先从红布袋中随机取出一个小球,记录其标有的数字为x,再从黄布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点M的一个坐标为(x.y)
(1)用列表或画树状图的方法写出点M的所有可能坐标;
(2)求点M落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第三象限的双曲线
在第三象限的双曲线![]() 上,过点
上,过点![]() 作
作![]() 轴交双曲线于点
轴交双曲线于点![]() ,连接
,连接![]() ,则
,则![]() 的面积为__________.
的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
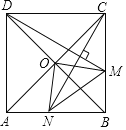
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正偶数按下表排成5列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
…… |
根据上面规律,2020应在( )
A.125行,3列B.125行,2列C.253行,2列D.253行,3列
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个箱子内有![]() 颗相同的球,将
颗相同的球,将![]() 颗球分别标示号码
颗球分别标示号码![]() ,
,![]() ,
,![]() ,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球
,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球![]() 次,现已取了
次,现已取了![]() 次,取出的号码依次为
次,取出的号码依次为![]() ,
,![]() ,
,![]() ,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球
,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球![]() 次,则发生“这
次,则发生“这![]() 次得分的平均数在
次得分的平均数在![]() 之间(含
之间(含![]() ,
,![]() )”的情形的概率为________.
)”的情形的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
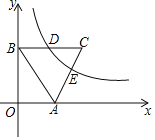
【题目】如图,在平面直角系中,点A在x轴正半轴上,点B在y轴正半轴上,∠ABO=30°,AB=2,以AB为边在第一象限内作等边△ABC,反比例函数的图象恰好经过边BC的中点D,边AC与反比例函数的图象交于点E.
(1)求反比例函数的解析式;
(2)求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
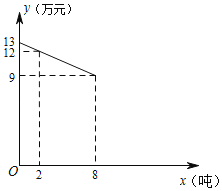
【题目】温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅,包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(2≤x≤10,单位:吨)之间的函数关系如图所示.
(1)若杨梅的销售量为6吨时,它的平均销售价格是每吨多少万元?
(2)当销售数量为多少时,该经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)
(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是y=![]() x+3(2≤x≤10).
x+3(2≤x≤10).
①当该公司买入杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?
②该公司买入杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com