
【题目】阅读下面的材料:
小明同学遇到这样一个问题,如图1,AB=AE,∠ABC=∠EAD,AD=mAC,点P在线段BC上,∠ADE=∠ADP+∠ACB,求![]() 的值.
的值.
小明研究发现,作∠BAM=∠AED,交BC于点M,通过构造全等三角形,将线段BC转化为用含AD的式子表示出来,从而求得![]() 的值(如图2).
的值(如图2).
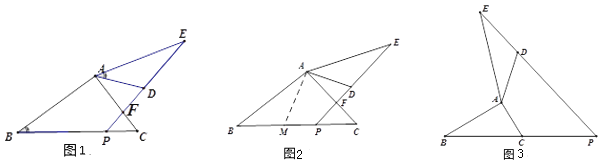
(1)小明构造的全等三角形是:_________≌________;
(2)请你将小明的研究过程补充完整,并求出![]() 的值.
的值.
(3)参考小明思考问题的方法,解决问题:
如图3,若将原题中“AB=AE”改为“AB=kAE”,“点P在线段BC上”改为“点P在线段BC的延长线上”,其它条件不变,若∠ACB=2α,求:![]() 的值(结果请用含α,k,m的式子表示).
的值(结果请用含α,k,m的式子表示).
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
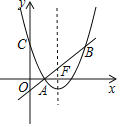
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,0),B两点,与y轴交于C(0,3),对称轴为直线x=2.
(1)请直接写出该抛物线的解析式;
(2)设直线l与抛物线的对称轴的交点为F,在对称轴右侧的抛物线上有一点G,若![]() ,且S△BAG=6,求点G的坐标;
,且S△BAG=6,求点G的坐标;
(3)若在直线![]() 上有且只有一点P,使∠APB=90°,求k的值.
上有且只有一点P,使∠APB=90°,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
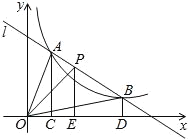
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
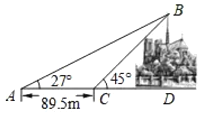
【题目】当地时间2019年4月15日下午,法国巴黎圣母院发生火灾,大火烧毁了巴黎圣母院后塔的塔顶.烧毁前,为测量此塔顶![]() 的高度,在地面选取了与塔底
的高度,在地面选取了与塔底![]() 共线的两点
共线的两点![]() 、
、![]() ,
,![]() 、
、![]() 在
在![]() 的同侧,在
的同侧,在![]() 处测量塔顶
处测量塔顶![]() 的仰角为27°,在
的仰角为27°,在![]() 处测量塔顶
处测量塔顶![]() 的仰角为45°,
的仰角为45°,![]() 到
到![]() 的距离是89.5米.设
的距离是89.5米.设![]() 的长为
的长为![]() 米,则下列关系式正确的是( )
米,则下列关系式正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
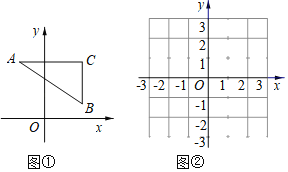
【题目】如图①,在平面直角坐标系中,当线段AB与坐标轴不垂直时,以线段AB为斜边作Rt△ABC,且边BC⊥x轴,则称AC+BC的值为线段AB的直角距离,记作L(AB);当线段AB与坐标轴垂直时,线段AB的直角距离不存在.
(1)在平面直角坐标系中,A(1,4),B(4,2),求L(AB).
(2)在平面直角坐标系中,点A与坐标原点重合,点B(x,y),且L(AB)=2.
①当点B(x,y)在第一象限时,易知AC=x,BC=y.由AC+BC=L(AB),可得y与x之间的函数关系式为 ,其中x的取值范围是 ,在图②中画出这个函数的图象.
②请模仿①的思考过程,分别探究点B在其它象限的情形,仍然在图②中分别画出点B在二、三、四象限时,y与x的函数图象.(不要求写出探究过程)
(3)在平面直角坐标系中,点A(1,1),在抛物线y=a(x﹣h)2+5上存在点B,使得2≤L(AB)≤4.
①当a=﹣![]() 时,直接写出h的取值范围.
时,直接写出h的取值范围.
②当h=0,且△ABC是等腰直角三角形时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个布袋,红布袋中有两个完全相同的小球,分别标有数字2和4.黄布袋中有三个完全相同的小球,分别标有数字﹣2,﹣4和﹣6.小贤先从红布袋中随机取出一个小球,记录其标有的数字为x,再从黄布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点M的一个坐标为(x.y)
(1)用列表或画树状图的方法写出点M的所有可能坐标;
(2)求点M落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() :
:![]() 和二次函数
和二次函数![]() :
:![]()
![]() 图象的顶点分别为
图象的顶点分别为![]() 、
、![]() ,与
,与![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)和
的左边)和![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),
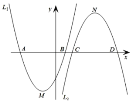
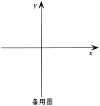
(1)函数![]() 的顶点坐标为______;当二次函数
的顶点坐标为______;当二次函数![]() ,
,![]() 的
的![]() 值同时随着
值同时随着![]() 的增大而增大时,则
的增大而增大时,则![]() 的取值范围是_______;
的取值范围是_______;
(2)判断四边形![]() 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)抛物线![]() ,
,![]() 均会分别经过某些定点;
均会分别经过某些定点;
①求所有定点的坐标;
②若抛物线![]() 位置固定不变,通过平移抛物线
位置固定不变,通过平移抛物线![]() 的位置使这些定点组成的图形为菱形,则抛物线
的位置使这些定点组成的图形为菱形,则抛物线![]() 应平移的距离是多少?
应平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
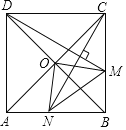
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com