
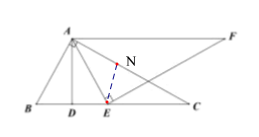
【题目】如图,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 为边
为边![]() 上的一个(不与
上的一个(不与![]() 、
、![]() 重合)点,且
重合)点,且![]() 于
于![]() 相交于点
相交于点![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)当![]() 时,证明:
时,证明:![]() .
.
(3)![]() 面积的最小值是_______.
面积的最小值是_______.
(4)当![]() 的内心在
的内心在![]() 的外部时,直接写出
的外部时,直接写出![]() 的范围______.
的范围______.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据锐角三角函数的定义以及三角形内角和定理,即可求解;
(2)由ASA,即可证明![]() ;
;
(3)由题意得:![]() 面积=
面积=![]() AE2,当AE⊥BC时,AE=
AE2,当AE⊥BC时,AE=![]() ,进而即可求解;
,进而即可求解;
(4)当![]() 的内心恰好落在AC上时,设
的内心恰好落在AC上时,设![]() 的内心为N,易证
的内心为N,易证![]() 是等边三角形,此时,AE=2,进而即可得到结论.
是等边三角形,此时,AE=2,进而即可得到结论.
(1)∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 180°-90°-60°=30°.
180°-90°-60°=30°.
故答案是:![]() ;
;
(2)![]() 于
于![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ;
;
(3)∵![]() =60°,
=60°,
∴EF=![]() AE,
AE,
∴![]() 面积=
面积= ![]() EFAE=
EFAE=![]() AE2,
AE2,
∴当AE的长最小时,![]() 面积的最小,即:AE⊥BC时,
面积的最小,即:AE⊥BC时,![]() 面积的最小.
面积的最小.
∴AE的最小值=ABsin60°=2×![]() =
=![]() ,此时,
,此时,![]() 面积的最小值=
面积的最小值=![]() .
.
故答案是:![]() .
.
(4)当![]() 的内心恰好落在AC上时,设
的内心恰好落在AC上时,设![]() 的内心为N,连接EN,
的内心为N,连接EN,
∵N是![]() 的内心,
的内心,
∴AN平分∠EAF,EN平分∠AEF,
∴∠EAC=![]() ∠EAF=30°,
∠EAF=30°,
∵∠BAC=90°,
∴∠BAE=∠BAC-∠EAC=90°-30°=60°,
又∵∠B=60°,
∴![]() 是等边三角形,
是等边三角形,
∴AE=AB=2,
∵![]() 为边
为边![]() 上的一个(不与
上的一个(不与![]() 、
、![]() 重合)点,由(1)可知
重合)点,由(1)可知![]() ,
,
∴当![]() 的内心在
的内心在![]() 的外部时,
的外部时,![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
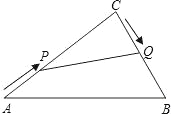
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )

A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:

(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以点C、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
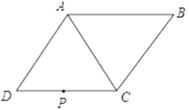
【题目】如图,在菱形ABCD中,∠ADC=60°,CD=4![]() cm,P为CD的中点.
cm,P为CD的中点.
(1)在AC上找一点Q,使DQ+PQ的值最小(保留画图痕迹,不写画法,不必说理);
(2)求出(1)中DQ+PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
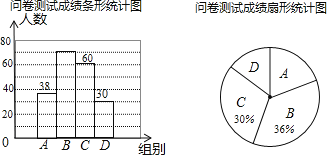
【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
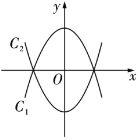
【题目】如图,已知拋物线![]() ,将抛物线
,将抛物线![]() 沿
沿![]() 轴翻折,得到拋物线
轴翻折,得到拋物线![]() .
.
(1)求出抛物线![]() 的函数表达式;
的函数表达式;
(2)现将抛物线![]() 向左平移
向左平移![]() 个单位长度,平移后得到的新抛物线的顶点为
个单位长度,平移后得到的新抛物线的顶点为![]() ,与
,与![]() 轴的交点从左到右依次为
轴的交点从左到右依次为![]() ,
,![]() ;将抛物线
;将抛物线![]() 向右也平移
向右也平移![]() 个单位长度,平移后得到的新抛物线的顶点为
个单位长度,平移后得到的新抛物线的顶点为![]() ,与
,与![]() 轴交点从左到右依次为
轴交点从左到右依次为![]() ,
,![]() .在平移过程中,是否存在以点
.在平移过程中,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是矩形的情形?若存在,请求出此时
为顶点的四边形是矩形的情形?若存在,请求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com