
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() ,则图中与
,则图中与![]() 全等的三角形(
全等的三角形(![]() 除外)有( ).
除外)有( ).
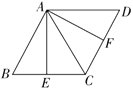
A.1个B.2个C.3个D.4个
【答案】C
【解析】
先由菱形的性质得出AD∥BC,由平行线的性质得到∠BAD+∠B=180°,又∠BAD=2∠B,求出∠B=60°,则∠D=∠B=60°,△ABC与△ACD是全等的等边三角形,再根据E,F分别为BC,CD的中点,即可求出与△ABE全等的三角形(△ABE除外)有△ACE,△ACF,△ADF.
解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B,AD∥BC,
∴∠BAD+∠B=180°,
∵∠BAD=2∠B,
∴∠B=60°,
∴∠D=∠B=60°,
∴△ABC与△ACD是全等的等边三角形,
∵E,F分别为BC,CD的中点,
∴![]() ,
,
在△ABE与△ACE中,
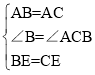
∴△ABE≌△ACE(SAS);
在△ABE与△ADF中,
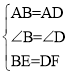
∴△ABE≌△ADF(SAS);
在△ABE与△ACF中,

∴△ABE≌△ACF(SAS);
∴图中与△ABE全等的三角形(△ABE除外)有3个,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
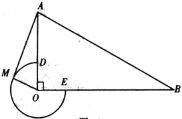
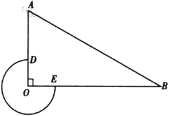
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
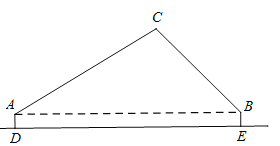
【题目】某数学小组在郊外的水平空地上对无人机进行测高实验.如图,两台测角仪分别放在A、B位置,且离地面高均为1米(即![]() 米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为
米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为![]() ,B处测得其仰角为
,B处测得其仰角为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)求该时刻无人机的离地高度;(单位:米,结果保留整数)
(2)无人机沿水平方向向左飞行2秒后到达点F(点F与点A、B、C在同一平面内),此时于A处测得无人机的仰角为![]() ,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
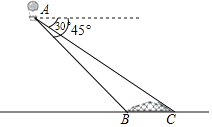
【题目】汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
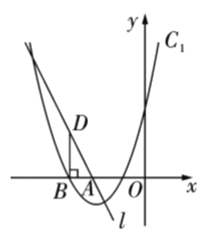
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 作
作![]() 垂直
垂直![]() 轴交直线
轴交直线![]() 于点
于点![]() .
.
(1)求抛物线的函数表达式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①求点![]() 的坐标;
的坐标;
②将拋物线![]() 向右平移使它经过点
向右平移使它经过点![]() ,此时得到的抛物线记为
,此时得到的抛物线记为![]() ,求出抛物线
,求出抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
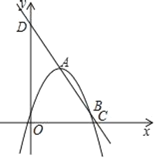
【题目】如图所示,二次函数y=k(x﹣1)2+2的图象与一次函数y=kx﹣k+2的图象交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0.
(1)求A、B两点的横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值;
(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
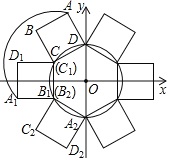
【题目】如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2)B.(2+![]() ,﹣1)
,﹣1)
C.(﹣1﹣![]() ,﹣1﹣
,﹣1﹣![]() )D.(1,﹣2﹣
)D.(1,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加射击比赛,10次射击的成绩如表:
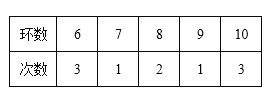
若小明再射击2次,分别命中7环、9环,与前10次相比,小明12次射击的成绩( )
A. 平均数变大,方差不变B. 平均数不变,方差不变
C. 平均数不变,方差变大D. 平均数不变,方差变小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com