
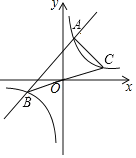
【题目】如图,已知函数![]() 的图象与函数
的图象与函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,连接
两点,连接![]() 并延长交函数
并延长交函数![]() 的图象于点
的图象于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为12,则
的面积为12,则![]() 的值为______.
的值为______.
【答案】![]()
【解析】
连接OA,根据反比例函数的对称性可得OB=OC,那么S△OAB=S△OAC=![]() S△ABC=6,求出直线y=x+3与y轴交点D的坐标,设A(a,a+3),B(b,b+3),则C(-b,-b-3),根据S△OAB=6,得出a-b=4①.根据S△OAC=6,得出-a-b=3②,①与②联立,求出a、b的值,即可求解.
S△ABC=6,求出直线y=x+3与y轴交点D的坐标,设A(a,a+3),B(b,b+3),则C(-b,-b-3),根据S△OAB=6,得出a-b=4①.根据S△OAC=6,得出-a-b=3②,①与②联立,求出a、b的值,即可求解.
解:如图,连接OA.
由题意,可得OB=OC,根据△ABC的面积为12,
∴S△OAB=S△OAC=![]() S△ABC=6,
S△ABC=6,
设直线y=x+3与y轴交于点D,则D(0,3),
设A(a,a+3),B(b,b+3),则C(-b,-b-3),
∴S△OAB=![]() ×3×(a-b)=6,
×3×(a-b)=6,
∴a-b=4①,
过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,
则S△OAM=S△OCN=![]() k,
k,
∴S△OAC=S△OAM+S梯形AMNC-S△OCN=S梯形AMNC=6,
∴![]() (-b-3+a+3)(-b-a)=6,
(-b-3+a+3)(-b-a)=6,
将①代入,得
∴-a-b=3②,
①+②,得-2b=7,b=-![]() ,
,
①-②,得2a=1,a=![]() ,
,
∴A(![]() ,
,![]() ),
),
∴k=![]() ×
×![]() =
=![]() .
.
故答案为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:

(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
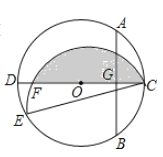
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.点E为圆上一点,∠ECD=15°,将![]() 沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
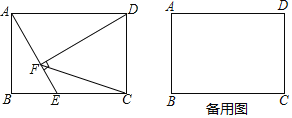
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() :
:![]() 和直线
和直线![]() :
:![]() ,点
,点![]() 和
和![]() 均在直线
均在直线![]() 上.
上.
(1)求直线![]() 的解析式;
的解析式;
(2)若抛物线过点![]() ,且抛物线与线段
,且抛物线与线段![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围;
的取值范围;
(3)将直线![]() 下移2个单位得到直线
下移2个单位得到直线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() 、
、![]() 两点,若点
两点,若点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“智慧校园”建设,某市准备为试点学校采购一批![]() 两种型号的一体机,经过市场调查发现,每套
两种型号的一体机,经过市场调查发现,每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多
型一体机的价格多![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买![]() 套
套![]() 型一体机和
型一体机和![]() 套
套![]() 型一体机.
型一体机.
(1)列二元一次方程组解决问题:求每套![]() 型和
型和![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)由于需要,决定再次采购![]() 型和
型和![]() 型一体机共
型一体机共![]() 套,此时每套
套,此时每套![]() 型体机的价格比原来上涨
型体机的价格比原来上涨![]() ,每套
,每套![]() 型一体机的价格不变.设再次采购
型一体机的价格不变.设再次采购![]() 型一体机
型一体机![]() 套,那么该市至少还需要投入多少万元?
套,那么该市至少还需要投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三个城市位置如图所示,A城在B城正南方向180 km处,C城在B城南偏东37°方向.已知一列货车从A城出发匀速驶往B城,同时一辆客车从B城出发匀速驶往C城,出发1小时后,货车到达P地,客车到达M地,此时测得∠BPM=26°,两车又继续行驶1小时,货车到达Q地,客车到达N地,此时测得∠BNQ=45°,求两车的速度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin26°≈
,sin26°≈![]() ,cos26°≈
,cos26°≈![]() ,tan26°≈
,tan26°≈![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com