
【题目】在平面直角坐标系![]() 中,点
中,点![]() 坐标是
坐标是![]() .当把坐标系绕点
.当把坐标系绕点![]() 顺时针选择30°时,点
顺时针选择30°时,点![]() 在旋转后的坐标系中的坐标是____;当把坐标系绕点
在旋转后的坐标系中的坐标是____;当把坐标系绕点![]() 逆时针选择30°时,点
逆时针选择30°时,点![]() 在旋转后的坐标系中的坐标是____.
在旋转后的坐标系中的坐标是____.
【答案】![]()
![]()
【解析】
根据题意,画出图形,连接AO,过点A作AB⊥x轴于点B,得AO=2,∠AOB=30°,当把坐标系绕点![]() 顺时针旋转30°时,相当于把OA绕点O逆时针旋转30°,当把坐标系绕点
顺时针旋转30°时,相当于把OA绕点O逆时针旋转30°,当把坐标系绕点![]() 逆时针旋转30°时,相当于把OA绕点O顺时针旋转30°,分别进行求解,即可.
逆时针旋转30°时,相当于把OA绕点O顺时针旋转30°,分别进行求解,即可.
连接AO,过点A作AB⊥x轴于点B,
∵点![]() 坐标是
坐标是![]() ,
,
∴AB=1,BO=![]() ,
,
∴AO=![]() =2,∠AOB=30°.
=2,∠AOB=30°.
∵当把坐标系绕点![]() 顺时针旋转30°时,相当于把OA绕点O逆时针旋转30°,
顺时针旋转30°时,相当于把OA绕点O逆时针旋转30°,
∴点![]() 在旋转后的坐标系中x轴的负半轴上,即:A(-2,0).
在旋转后的坐标系中x轴的负半轴上,即:A(-2,0).
∵当把坐标系绕点![]() 逆时针旋转30°时,相当于把OA绕点O顺时针旋转30°,
逆时针旋转30°时,相当于把OA绕点O顺时针旋转30°,
∴∠B′OA′=60°,OA′=OA=2,
∴A′B′= OA′×sin60°=2×![]() =
=![]() ,OB′= OA′×cos60°=2×
,OB′= OA′×cos60°=2×![]() =1,
=1,
∴![]() .
.
故答案是:![]() ;
;![]() .
.
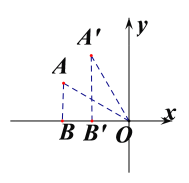


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
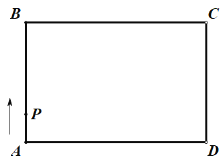
【题目】如图,在矩形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿着矩形的边顺时针方向运动一周回到点
出发,沿着矩形的边顺时针方向运动一周回到点![]() ,则点
,则点![]() 围成的图形面积
围成的图形面积![]() 与点
与点![]() 运动路程
运动路程![]() 之间形成的函数关系式的大致图象是( )
之间形成的函数关系式的大致图象是( )
A.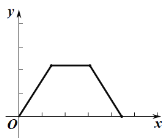 B.
B.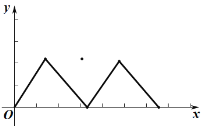
C.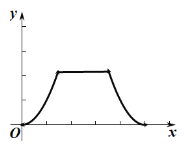 D.
D.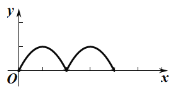
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某数学小组在学完《直角三角形的边角关系》这章后,决定用所学的知识设计遮阳篷(要求:遮阳篷既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内).他们制定了设计方案,并利用课余时间完成了调查和实地测量.调查和测量项目及结果如下表:
项目 | 内容 | |
课题 | 设计遮阳篷 | |
测量示意图 |
| 如图,设计了垂直于墙面AC的遮阳篷CD,AB表示窗户的高度.榆次区一年中,夏至这一天的正午时刻,太阳光线DA与遮阳篷CD的夹角∠ADC最大;冬至这一天的正午时刻,太阳光线DB与遮阳篷CD的夹角∠CDB最小. |
调查数据 |
|
|
测量数据 |
| |
… | … | |
根据上述方案及数据,求遮阳篷![]() 的长.
的长.
(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为_____,表示“D等级”的扇形的圆心角为_____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
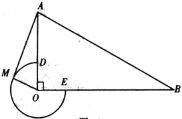
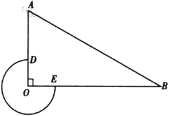
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数![]() 在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1。直线l过O、E两点,则tan∠EOC的值为( )
在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1。直线l过O、E两点,则tan∠EOC的值为( )

A. ![]() B. 5 C.
B. 5 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
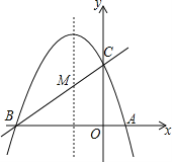
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
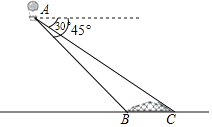
【题目】汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com