
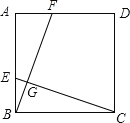
【题目】如图,在正方形ABCD中,点E,F分别为AB,AD的中点,CE,BF相交于点G,AB=2,则CG=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先根据题意证明△AFB≌△BEC,可得∠EGB=90°,在Rt△CBE中即可求出tan∠ECB,所以在Rt△BCG中,设BG=x,CG=2x,根据勾股定理求解即可得答案.
在正方形ABCD中,BC=AB=2,∠A=∠EBC=90°,
∵点E,F分别为AB,AD的中点,
∴AF=BE=1,
在△AFB与△BEC中,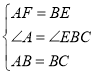 ,
,
∴△AFB≌△BEC(SAS),
∴∠FBA=∠ECB,
∵∠ECB+∠BEC=∠FBA+∠BEC=90°,
∴∠EGB=90°,
在Rt△CBE中,tan∠ECB![]() ,
,
在Rt△BCG中,设BG=x,CG=2x,
由勾股定理可知:x2+4x2=4,
解得:x![]() ,
,
∴CG![]() ,
,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0),(3,0)两点,则下列判断中,错误的是( )

A.图象的对称轴是直线x=1
B.当﹣1<x<3时,y<0
C.当x>1时,y随x的增大而减小
D.一元二次方程中ax2+bx+c=0的两个根是﹣1和3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtABC中,∠ACB=90°,以AC为直径的⊙O与边AB交于点D,过点D作⊙O的切线,交BC于E.

(1)求证:点E是边BC的中点;
(2)求证:BC2=BDBA;
(3)当AC=BC时,四边形OCED是什么四边形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:点(x,y)在直线y=﹣x+1上,且x2+y2=2,求x7+y7的值.
(2)计算:
![]()
(3)已知a、b、c是直角三角形△ABC的角A、B、C所对的边,∠C=90°.求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点,已知反比例函数y=![]() (m<0)与y=x2﹣5在第四象限内围成的封闭图形(包括边界)内的整点的个数为4,则实数m的取值范围为_____.
(m<0)与y=x2﹣5在第四象限内围成的封闭图形(包括边界)内的整点的个数为4,则实数m的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
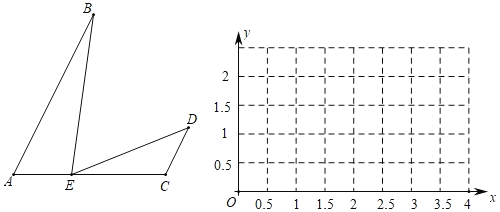
【题目】如图,AB∥CD,AB=5cm,AC=4cm,线段AC上有一动点E,连接BE,ED,∠BED=∠A=60°,设A,E两点间的距离为xcm,C,D两点间的距离为ycm.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.3 | 2.5 |
y/cm | 0 | 0.39 | 0.75 | 1.07 | 1.33 | 1.45 |
|
x/cm | 2.8 | 3.2 | 3.5 | 3.6 | 3.8 | 3.9 | |
y/cm | 1.53 | 1.42 | 1.17 | 1.03 | 0.63 | 0.35 |
请你补全表格;
(2)描点、连线:在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象;
(3)探究性质:随着自变量x的不断增大,函数y的变化趋势: ;
(4)解决问题:当AE=2CD时,CD的长度大约是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
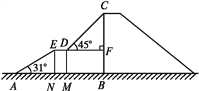
【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转一定角度后能与△DFA重合.
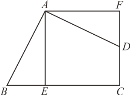
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5cm,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a =2;④方程ax2+bx+c=0有两个相等的实数根.其中正确结论的个数为( )
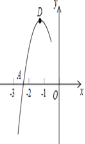
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com